
|
||
|
|
||
|
|
Онлайн книга - Увлекательно о космосе. Межпланетные путешествия | Автор книги - Яков Перельман
Cтраница 41

Для решения первой задачи представим себе, что на 0,9 расстояния от Земли до Луны обращается вокруг нашей планеты небесное тело, и вычислим период обращения этого воображаемого спутника Земли. Обозначив неизвестный период обращения через х, составляем на основании третьего Кеплерова закона пропорцию 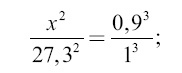
отсюда искомый период обращения
Разделив этот период на √32, то есть на 5,6, мы, согласно выведенному ранее правилу, получим время перелета снаряда от Земли до нейтральной точки: 23,3: 5,6 = 4,1 сут. Вторую задачу решаем сходным образом. Чтобы вычислить, за сколько времени снаряд упал бы с расстояния нейтральной точки до Луны, нужно сначала определить, за сколько времени снаряд, находясь на том же расстоянии от Луны, совершил бы вокруг нее полный оборот. Радиус орбиты этого воображаемого спутника Луны равен 0,1 радиуса лунной орбиты, а масса центрального светила (в данном случае Луны) в 81 раз меньше массы Земли. Если бы масса Луны равнялась земной, то спутник, обращаясь на среднем расстоянии вдесятеро меньшем, чем лунное, совершил бы полный оборот в период у, легко вычисляемый по закону Кеплера: 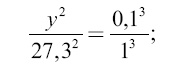
откуда 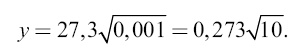
Но так как масса, а следовательно, и притягательное действие центрального светила в данном случае в 81 раз меньше, чем в системе Земли, то время обращения снаряда-спутника будет дольше. Во сколько раз? Из механики мы знаем, что центростремительное ускорение пропорционально квадрату скорости. Здесь это ускорение (производимое притяжением Луны) меньше в 81 раз, следовательно, скорость движения снаряда по орбите должна быть меньше в √81 раз, то есть в 9 раз. Другими словами, снаряд в роли лунного спутника должен обегать кругом Луны в 9 раз медленнее, чем он обходил бы на таком же расстоянии вокруг Земли. Значит, искомое время обращения равняется: 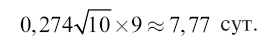
Чтобы получить продолжительность падения снаряда от нейтральной точки до Луны, нужно, как мы уже знаем, найденный сейчас период его обращения (7,77) разделить на √32, то есть на 5,6; получим 1,4 сут., а точнее – 33,5 ч. [46] Итак, весь перелет пушечного снаряда от Земли до Луны должен был бы длиться 4,1 + 1,4 сут. = 5,5 сут. Однако это не вполне точный результат: здесь не принято во внимание то обстоятельство, что и при полете от Земли до нейтральной точки снаряд подвергается притягательному действию Луны, которое ускоряет его движение; с другой стороны, при падении на Луну он испытывает на себе замедляющее действие земного притяжения. Последнее действие должно быть особенно заметно и, как показывает более точное вычисление (по формуле, приведенной ниже), примерно вдвое увеличило бы продолжительность падения снаряда от нейтральной точки до Луны. Благодаря этим поправкам общая продолжительность перелета снаряда от Земли до Луны с 5,5 суток возрастает до 7 суток. В романе продолжительность перелета определена «астрономами Кэмбриджской обсерватории» в 97 ч. 13 мин. 20 с, то есть в 4 с небольшим суток вместо 7 суток. Жюль Верн ошибся на трое суток. Ошибка произошла от того, что романист (или лицо, производившее для него расчеты) преуменьшил время падения снаряда от нейтральной точки до Луны: оно определено всего в 13 ч. 53 мин., между тем как это падение должно было совершиться гораздо медленнее и отнять 67 ч. Если тело падает без начальной скорости с весьма большого расстояния H не до центра притяжения, а до некоторого расстояния h, то продолжительность t (в секундах) такого падения вычисляется по следующей формуле, которая выводится в курсах интегрального исчисления: 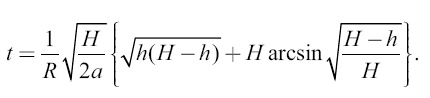
Здесь H и h имеют указанные выше значения, R – радиус планеты, а — ускорение тяжести на ее поверхности. По этой формуле вычисляется также продолжительность взлета тела от расстояния h до расстояния Н, где оно должно утратить всю свою скорость. Для примера вычислим продолжительность взлета тела, брошенного с земной поверхности на высоту земного радиуса. В этом случае Н = 2R; h = R; а = g = 9,8; R = 6370. Имеем продолжительность взлета: 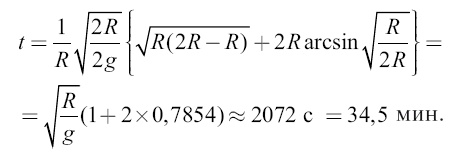
Значит, ракета, пущенная вверх на расстояние земного радиуса, должна возвратиться через 69 мин. 3. Динамика ракеты
Для понимания дальнейшего необходимо отчетливо уяснить себе некоторые теоремы механики, относящиеся к количеству движения и к центру тяжести. Предпосылаем поэтому нашему изложению небольшую главу из «Курса физики» Гримзеля, где положения эти разъяснены весьма наглядно и с достаточной полнотой. Импульс. Количество движения. Сохранение движения центра тяжести «Сила Р сообщает свободной массе m ускорение а, которое определяется из уравнения Р = ma. Если сила Р постоянна, то и ускорение постоянно, т. е. движение равномерно-ускоренное. Если постоянная сила Р действует на массу m в течение времени t, то она сообщает ей скорость υ = at. Чтобы оценить действие силы Р за время t, мы умножим выражение силы Р = ma на t. Мы получим равенство Р × t = m × υ.
|
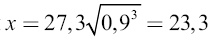 .
. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно