Увлекательно о космосе. Межпланетные путешествия - читать онлайн книгу. Автор: Яков Перельман cтр.№ 40

Гений Ньютона открыл человечеству закон действия могучей силы, приковывающей нас к Земле. Но тот же гений провозгласил и другой закон природы, опираясь на который человек свергнет иго тяжести и вырвется из земного плена на простор Вселенной, в необъятный мир миров.

Приведенные в главе 2 примеры действия силы тяготения могут быть проверены несложными расчетами, основанными на законе Ньютона и элементах механики. Читатели, имеющие начальные сведения из алгебры, без затруднения проследят за ними. Напомним, что за единицу измерения силы в механике принята сила, которая, будучи приложена к свободному телу массою в 1 г, ежесекундно увеличивает его скорость на 1 см/с. Эта единица силы называется диной. Так как сила земного притяжения ежесекундно увеличивает скорость свободно падающего грамма почти на 1000 см/с (9,8 м/с), то сила, с какой притягивается к Земле 1 г, больше дины почти в 1000 раз, то есть равна (почти) 1000 дин. Другими словами, вес гирьки в 1 г (сила ее притяжения к Земле) равен почти 1000 дин. Это дает представление о величине дины в единицах веса: дина равна примерно ¹/₁₀₀₀ г.

Далее: установлено, что два шарика, по 1 г каждый, расстояние между центрами которых равно 1 см, притягиваются между собой с силою в ¹/_15000000 дины. Эту величину называют «постоянной тяготения».

После сказанного нетрудно, на основании закона Ньютона, вычислить силу взаимного притяжения двух человеческих тел, разделенных промежутком в 1 м (или 100 м). Принимая вес человеческого тела в 65 кг (65 000 г) и имея в виду, что взаимное притяжение прямо пропорционально произведению масс и обратно пропорционально квадрату расстояния (закон Ньютона), имеем для силы взаимного притяжения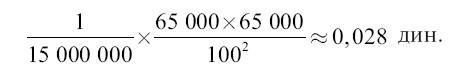

Итак, два человеческих тела на расстоянии 1 м притягиваются взаимно с силою 0,028 дины (около ¹/₄₀ мг).

Таким же образом может быть вычислена сила взаимного притяжения и двух линейных кораблей, разделенных расстоянием 1 км. Масса каждого корабля равна 25 000 т = 25 000 000 000 г; расстояние равно 100 000 см. Поэтому взаимное притяжение равно: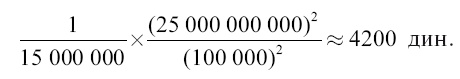

Так как 1000 дин = 1 г, то 4200 дин равны примерно 4 г.

Полет пушечного снаряда Жюля Верна на Луну можно рассматривать как случай падения тела в мировом пространстве под влиянием силы тяготения. Поэтому, прежде чем рассматривать условия его полета, полезно рассмотреть следующую задачу из области небесной механики.

Во сколько времени упал бы на Солнце земной шар, если бы от какой-нибудь причины прекратилось его движение по орбите?

Задачи подобного рода легко разрешаются на основании третьего закона Кеплера: квадраты времен обращения планет и комет относятся как кубы их средних расстояний от Солнца; среднее же расстояние от Солнца равно длине большой полуоси эллипса. В нашем случае мы можем земной шар, падающий прямо на Солнце, уподобить воображаемой комете, движущейся по сильно вытянутому эллипсу, крайние точки которого расположены: одна – близ земной орбиты, другая – в центре Солнца. Среднее расстояние такой кометы от Солнца, то есть большая полуось ее орбиты, очевидно, вдвое меньше среднего расстояния Земли. Вычислим, каков должен был бы быть период обращения этой воображаемой кометы. Составим на основании третьего закона Кеплера пропорцию: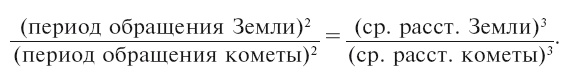

Период обращения Земли равен 365 суткам; среднее расстояние ее от Солнца примем за единицу, и тогда среднее расстояние кометы выразится через ½. Пропорция принимает вид: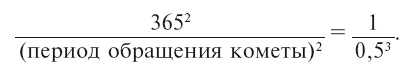

Откуда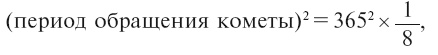

или

Но нас интересует не полный период обращения этой воображаемой кометы, а половина периода, то есть продолжительность полета в один конец – от земной орбиты до Солнца: это и есть искомая продолжительность падения Земли на Солнце. Она равна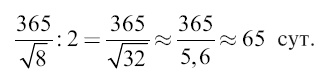

Итак, чтобы узнать, за сколько времени Земля упала бы на Солнце, нужно продолжительность года разделить на √32, то есть на 5,6. Легко видеть, что полученное простое правило применимо не к одной только Земле, но и ко всякой другой планете и ко всякому спутнику. Иначе говоря, чтобы узнать, за сколько времени планета или спутник упадут на свое центральное светило, нужно период их обращения разделить на √32, то есть на 5,6. Меркурий, обращающийся за 88 дней, упал бы на Солнце за 15,5 дня; Сатурн, период обращения которого равняется 30 нашим годам, падал бы на Солнце в течение 5,5 года. А Луна упала бы на Землю за 27,3: 5,6, то есть за 4,8 сут. И не только Луна, но и всякое вообще тело, находящееся от нас на расстоянии Луны, падало бы к Земле в течение 4,8 сут. (если только ему не сообщена начальная скорость, а падает оно, подчиняясь лишь действию одного земного притяжения).

Здесь мы вплотную подходим к задаче Жюля Верна. Легко понять, что столько же времени должно лететь на Луну всякое тело, брошенное с Земли на Луну с такою скоростью, чтобы пройти как раз расстояние до Луны. Значит, алюминиевый снаряд Жюля Верна должен был бы лететь около 5 суток, если бы его хотели закинуть на расстояние Луны.

Однако члены Пушечного клуба рассчитывали закинуть снаряд не прямо на Луну, а только до той точки между Землей и Луной, где силы притяжения обоих светил уравниваются: отсюда снаряд сам уже упал бы на Луну, притягиваемый ею. Эта нейтральная точка находится на 0,9 расстояния от Земли.

Вычисление, следовательно, несколько усложняется. Во-первых, нужно вычислить, за сколько времени снаряд долетел бы до 0,9 расстояния между Землей и Луной или, что то же самое, за сколько времени тело с этого расстояния упало бы на Землю; во-вторых, надо определить продолжительность падения тела от этой нейтральной точки до Луны.