Битва при черной дыре. Мое сражение со Стивеном Хокингом за мир, безопасный для квантовой механики - читать онлайн книгу. Автор: Леонард Сасскинд cтр.№ 82

Чтобы Лайнландия стала интереснее, нам надо добавить в нее объекты, так что создадим частицы, которые движутся вдоль линии.

Думайте о них как о крошечных бусинах, которые сцепляются друг с другом, образуя одномерные атомы, молекулы и, возможно, даже живых существ. (Я сильно сомневаюсь, что жизнь может существовать в мире с одним измерением, но давайте пока подержим эти сомнения при себе.) Считайте и линию, и бусины бесконечно тонкими, так что они не высовываются в другие измерения. А лучше даже попытаться представить себе линию с бусинами вообще без других измерений ^[134].

Сообразительный человек придумает много альтернативных версий Лайнландии. Все бусины могут быть одинаковыми, или, в более интересном мире, может существовать несколько разных типов бусин. Чтобы различать эти типы, пометим их цветами — красным, синим, зеленым и т. д. Я могу представить себе бесчисленно множество возможностей: красные бусины притягивают синие, но отталкивают зеленые. Черные бусины очень тяжелые, а белые — безмассовые и движутся по Лайнландии со скоростью света. Можно даже позволить бусинам быть квантово-механическими, цвет каждой отдельной бусины может быть неопределенным.

Жизнь в одном-единственном измерении очень стесненная. Имея свободу двигаться только вдоль одной линии, лайнландцы непременно будут сталкиваться друг с другом. Смогут ли они общаться? Легко: для отправки сообщений они могут перебрасываться бусинами, находящимися у их концов. Однако их социальная жизнь очень уныла: каждое существо имеет лишь двоих знакомых — одного справа и одного слева. Нужно по меньшей мере два измерения, чтобы сформировать социальный круг.

Но внешность обманчива. Когда лайнландцы смотрят в очень сильный микроскоп, они начинают обнаруживать, что их мир в действительности двумерный. Они видят не идеальную математическую линию нулевой толщины, а скорее поверхность цилиндра. В обычных обстоятельствах окружность этого цилиндра слишком мала, чтобы лайнландцы могли ее обнаружить, но под микроскопом удалось открыть куда более мелкие объекты, меньше даже, чем лайнландские атомы. Эти объекты столь малы, что могут двигаться в двух измерениях.

Подобно своим братьям-великанам, эти лайнландские карлики могут перемещаться вдоль цилиндра, но они достаточно малы, чтобы обходить по его окружности. Они способны даже двигаться одновременно по обоим направлениям, накручивая спиральные витки вокруг цилиндра. И — о, радость! — они могут даже обходить друг друга без столкновений. Вполне резонно они утверждают, что живут в двумерном пространстве, но с одной особенностью: если двигаться по прямой линии в дополнительном измерении, то скоро вернешься в исходную точку.

Лайнландцам понадобилось название для нового направления, и они обозначили его Y. В отличие от Х, вдоль Y нельзя далеко уйти, не вернувшись в исходную точку. Лайнландские математики говорят, что направление Y компактифицировано.

Цилиндр, изображенный выше, получается при добавлении дополнительного свернутого измерения к исходному одномерному миру. Добавление шести дополнительных измерений к миру, в котором уже есть три обычных, выходит далеко за пределы способностей человеческого мозга к визуализации. Физиков и математиков отличает от остальных людей не то, что они мутанты, способные представить себе любое число измерений, а скорее то, что они прошли тяжелую математическую переподготовку, опять же, перепрошивающую сознание, — чтобы научиться «видеть» дополнительные измерения.

Единственное дополнительное измерение не обеспечивает достаточного разнообразия возможностей. Перемещение в свернутом направлении будет подобно движению по кругу без осознания этого. Но уже два дополнительных измерения открывают бесконечное множество новых возможностей. Два измерения могут образовать сферу.

тор (поверхность бублика),

бублик с двумя или тремя дырками,

или даже причудливое пространство, называемое бутылкой Клейна.

Изображение двух дополнительных измерений не составляет больших проблем (мы только что сделали это), но с ростом числа измерений визуализировать их становится все труднее и труднее. К тому моменту когда мы достигнем шести дополнительных измерений, необходимых для теории струн, визуализация без обращения к математике становится безнадежным делом. Особые геометрические пространства, которые струнные теоретики используют для компактификации шести дополнительных измерений, называются многообразиями Калаби — Яу. Их насчитываются миллионы, и среди них нет двух одинаковых. Многообразия Калаби — Яу исключительно сложны, с сотнями шестимерных дырок от бубликов и прочими невообразимыми кренделями. Тем не менее математики создают их изображения, нарезая на слои меньшей размерности, подобно диаграммам вложения ^[135]. Вот изображение двумерного среза типичного пространства Калаби — Яу.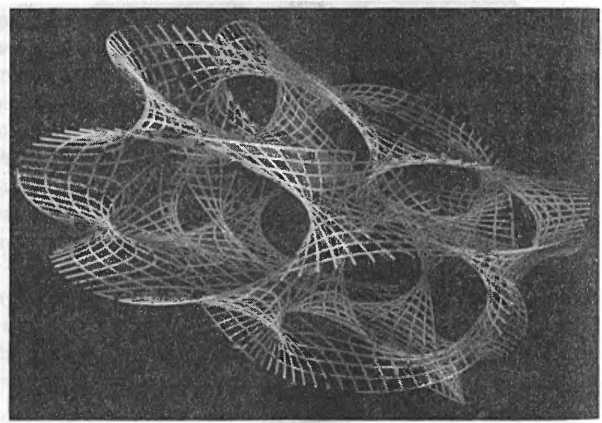

Я попробую дать вам некоторое представление о том, на что похоже обычное пространство, когда к каждой его точке добавлено шестимерное многообразие Калаби — Яу. Сначала посмотрите на обычные измерения, в которых могут двигаться такие большие объекты, как люди. (Я нарисовал его двумерным, но вы уже должны научиться достраивать третье измерение в воображении.)