Стратегии решения математических задач. Различные подходы к типовым задачам - читать онлайн книгу. Автор: Стивен Крулик, Альфред Позаментье cтр.№ 38

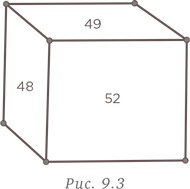
Большинство людей замечают, что числа на гранях куба начинаются с 48 и 49. Чаще всего они просто продолжают числовой ряд и получают следующие номера на гранях: 48, 49, 50, 51, 52, 53. Поскольку номер третьей грани, а именно 52, присутствует в этой последовательности, некоторые останавливаются и дают в качестве ответа сумму перечисленных номеров — 303.

Вместе с тем в приведенном выше решении учтены не все возможности. Мы видим три грани из шести. Поскольку нам видны номера 48, 49 и 52, значит обязательно должны быть 50 и 51. Шестой номер, однако, может находиться на любом конце последовательности. Таким образом, существуют два варианта шестого номера — 47 или 53. Это дает две возможные суммы — 297 и 303.

Конечно, даже мысль о том, что в качестве стратегии решения задач можно использовать догадки, вызывает недоумение. В самом деле, может ли кто из нас вспомнить, чтобы учитель говорил кому-то, давшему нестандартный ответ: «Ты это знаешь или просто строишь догадки?» В некоторых книгах выдвижение предположений и их проверку называют методом «проб и ошибок», и это воспринимается более негативно. Добавление определения обоснованное в название метода должно успокоить вас и уверить в том, что это действительно эффективная и нередко очень полезная стратегия.

Мы пользуемся стратегией «предположение-и-проверка» на протяжении всей своей жизни. Например, на кухне мы делаем предположение о том, готово ли мясо в духовке, а потом с помощью специального термометра проверяем, правильно ли оно. Если нет, то мясо опять отправляется в духовку, а процесс «предположение-проверка» повторяется через некоторое время. Пытаясь найти конкретное место во время поездки на автомобиле, мы «предполагаем», что оно находится на определенной улице. Если его там нет, то мы делаем другое предположение на основе информации, полученной в результате первой попытки.

При решении задач, когда слишком много неопределенностей, мы можем использовать эту стратегию для уменьшения неопределенности с помощью конкретных предположений. Проверяя предположения, мы получаем информацию для уточнения следующего предположения и приближаемся к отысканию ответа.

Чтобы помогать решению задач, предположения должны быть неслучайными и не взятыми с потолка без очевидного основания. После изучения условий задачи определяется возможный подход к решению и выдвигается предположение. Затем предположение проверяется на основе условий задачи. Если это не приводит к получению ответа, то выдвигается следующее предположение с учетом информации, полученной на предыдущем этапе. Новое предположение опять проверяется. Процесс уточнения предположений продолжается до тех пор, пока не будет накоплена информация, достаточная для решения задачи. Например, предположим, что нас просят найти следующие два члена последовательности 2, 0, 4, 3, 6, 7, 8, 12, 10, 18, ____, ____. Что мы видим? Возможно, члены последовательности возрастают и уменьшаются случайным образом. Не исключено, что здесь смешаны две последовательности. Это выглядит как обоснованное предположение. Попробуем проверить его!

Похоже, что наше предположение правильно — здесь действительно две последовательности. Последовательность 1 состоит из четных чисел. Следующим ее членом будет 12. В последовательности 2 разность между последовательными членами возрастает каждый раз на 1, т. е. разности равны 3, 4, 5, 6 и т. д. Следующий ее член должен быть равен 25. Таким образом, мы получаем ответ: следующие два члена — это 12 и 25. Обратите внимание на то, что здесь использовалась также стратегия выявления закономерности. В применении нескольких стратегий для решения задачи нет ничего необычного.

Обратите внимание также, что предположения берутся не с потолка. Все они основываются на тщательном анализе того, что дано, и того, что требуется найти. Предположения делаются с умом! Не забывайте, что эту стратегию не случайно называют «обоснованным предположением и проверкой».

Рассмотрим еще один пример использования этой стратегии.

Вместо привычного составления уравнений попробуем воспользоваться стратегией выдвижения обоснованного предположения и его проверки. Для отслеживания наших предположений составим таблицу. Начнем с середины — с 25 шаров каждого вида.

В коробку следует положить 30 сплошных шаров и 20 полых. Если попробовать все сочетания подряд, то они все равно приведут к правильному ответу. Выдвижение обоснованных предположений позволяет сократить количество попыток.

Рассмотрим еще одну задачу, решение которой сильно выигрывает от применения нашей стратегии.

Поскольку нужно найти минимальное количество дротиков, секций с высокими значениями должно быть как можно больше. Сделаем несколько предположений и представим результаты в табличной форме.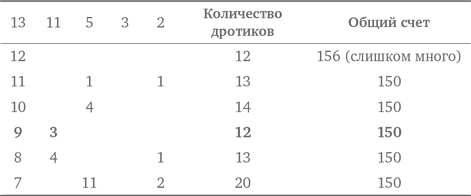

Наименьшее количество дротиков, которые могли потребоваться Памеле, равно 12. Обратите внимание на то, что мы опять использовали стратегию организации данных для отслеживания результатов оценки предположений. Табличное представление данных нередко очень облегчает анализ полученной информации.

На местной ферме выращивают голубику, кусты которой высажены так, что они образуют решетку с квадратными ячейками, а количество рядов равно количеству колонок. Фермер решил увеличить размеры поля на одинаковое количество рядов и колонок. Новое поле вмещает на 211 кустов больше, чем старое. Сколько кустов было в одном ряду на старом поле?