
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 35

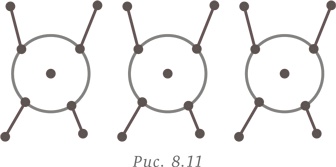
До нужной величины нам не хватает шести ног — их необходимо добавлять парами (рис. 8.11). У нас получилось три четвероногих фигурки и семь двуногих. Осталось умножить их на 10. Таким образом, мы получаем 30 фигурок буйволов и 70 фигурок обезьян. 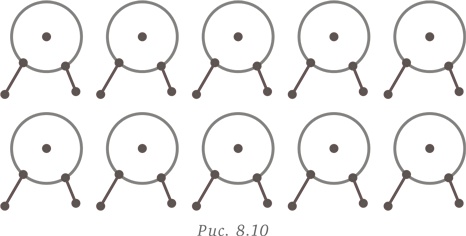
Глава 9
Учет всех возможностей Мы знаем, что организация данных иногда очень облегчает поиск решения. Если нужно выявить, например, закономерность, то аккуратное представление данных в виде списка или таблицы может помочь в этом. Особенно интересны здесь исчерпывающие списки, т. е. списки, в которых систематизированно перечисляются все существующие возможности. В таких списках часто обнаруживается то, что мы ищем. Составление исчерпывающего списка позволяет тщательно проанализировать все возможности. В качестве примера предположим, что у вас не работает лампа. Попробуем перечислить все возможности. (Конечно, это можно сделать мысленно, но в результате вы все равно получите список.) Проблема может крыться в перегоревшей лампочке, оборванном проводе, неработающей розетке, сработавшем предохранителе или неисправном выключателе. Проверяя возможности одну за другой, мы в конечном итоге дойдем до той, которая является причиной неисправности. Математический пример может выглядеть так: Имеется двузначный квадрат целого числа. Если вставить одну цифру между существующими двумя, то получится трехзначный квадрат целого числа. Какие трехзначные квадраты чисел мы получаем? Проанализируем все возможности. Прежде всего, составим исчерпывающий список двузначных квадратов целых чисел, их шесть: 16, 25, 36, 49, 64, 81. Теперь составим исчерпывающий список трехзначных квадратов целых чисел: 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961. Выберем из второго списка те числа, которые можно составить, вставив какую-либо цифру между первой и второй цифрами двузначных квадратов целых чисел. Такому условию удовлетворяют только 196 (вставлена 9 между цифрами числа 16), 225 (вставлена 2 между цифрами числа 25) и 841 (вставлена 4 между цифрами числа 81). Два исчерпывающих списка сделали очевидными все возможности. Обратите внимание на то, что исчерпывающий список не только содержит ответ задачи, но ограничивает количество исследуемых возможностей. Вот еще один пример использования этой полезной стратегии. На скамейке в парке сидят два человека. Один из них — женщина. Какова вероятность того, что и второй тоже окажется женщиной? Составим список всех возможностей (М = мужчина, Ж = женщина): М — М М — Ж Ж — М Ж — Ж. В список пошли четыре возможности, однако в нашей задаче первую, М — М, не нужно учитывать, поскольку известно, что как минимум один человек — женщина. У нас остаются три варианта, и лишь в одном из них могут быть две женщины. Таким образом, ответом на поставленный вопрос будет вероятность, равная. Чтобы еще лучше увидеть ценность такого подхода к решению задач, рассмотрим еще один пример: В двух залах местного кинотеатра показывают по утрам разные мультфильмы. Утренние сеансы в обоих залах должны заканчиваться к 13:00, когда начинается демонстрация художественных фильмов. В зале A первый сеанс мультфильмов начинается в 9:00, второй в 9:28, а потом через каждые 28 минут. В зале B первый сеанс тоже начинается в 9:00, но потом сеансы повторяются через 35 минут. Джоанн хочет попасть на просмотр мультфильмов в обоих залах. Во сколько два последующих сеанса начинаются одновременно? Составим исчерпывающий список времени начала сеансов в обоих залах. 
Любой последующий сеанс должен был бы начаться уже после 13:00. Мы перечислили все возможности! Где-то в этом списке всех должен находиться ответ. Список показывает лишь одно время, когда начало сеансов в обоих залах совпадает — 11:20. Такая стратегия очень эффективна, но вы должны убедиться в том, что перечислили все без исключения возможности! Только тщательная организация данных может дать вам полную уверенность. Как и в случае с другими стратегиями, необходимо обдуманно подходить к выбору той, которая подходит в данном случае. Стратегия учета всех возможностей может сделать решение более очевидным. Задача 9.1
Учитель математики замечает, что его нынешний возраст представляет собой простое число. Он обнаруживает, что в следующий раз его возраст станет простым числом через столько же лет, сколько прошло с той поры, когда возраст был простым числом в прошлый раз. Сколько лет учителю математики? Обычный подход
У этой задачи не так много альтернативных способов решения. Обычно начинают перебирать числа в надежде «наткнуться на подходящее». Образцовое решение
Здесь наверняка нам пригодится стратегия учета всех возможностей. Рассмотрим следующий список: 
В списке простых чисел от 1 до 100 (хотя в ситуации учителя математики можно было бы ограничиться числами в диапазоне от 20 до 80) только в двух случаях три последовательных простых числа имеют одинаковую разность. Первый случай — 3, 5 и 7 — нам не подходит, поскольку пятилетних учителей математики не бывает. Второй случай — 47, 53 и 59 — укладывается в подходящий возрастной диапазон. Таким образом, учителю математики должно быть 53 года. Задача 9.2
Найдите количество сочетаний, при которых 20 монет достоинством 5 центов, 10 центов и 25 центов могут составить в сумме $3,10. Обычный подход
Большинство людей сразу начинают составлять алгебраические уравнения, отражающие информацию из условий задачи. В результате они получают: n + d + q = 20, где n, d и q — количество 5-, 10- и 25-центовых монет соответственно. Это можно записать, как n = 20 — q — d. Кроме того, 25q + 10d + 5n = 310, что при объединении с предыдущими двумя уравнениями дает: 25q + 10d + 5 (20 — q — d) = 310. Отсюда 4q + d = 42, или
|
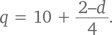 После этого остается лишь подставлять разные значения, чтобы выявить наилучший результат.
После этого остается лишь подставлять разные значения, чтобы выявить наилучший результат. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно