
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 36

Образцовое решение
У нас, однако, есть более рациональный метод, а именно учет всех возможных значений d. Прежде всего, мы замечаем, что q должно быть целым числом, а значит необходимо выделить дробную часть q, т. е.
Поскольку d = 2–4k, значение k может быть либо нулевым, либо отрицательным. В таблице ниже приведены возможные значения k и вытекающие из него значения d, q и n. 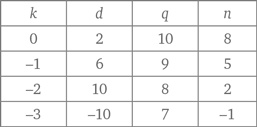
При k = 0, –1, –2 мы получаем реальные варианты. Когда же k = –3, d = 2–4(–3) = 14, а n = 8 + 3(–3) = –1, что не имеет смысла в этой задаче. Таким образом, количество сочетаний, при которых сумма составляет $3,10, равно трем. Задача 9.3
Для доставки консервов из тунца компания может использовать небольшие коробки, в которые входит восемь банок, и коробки побольше, вмещающие 10 банок. С целью экономии компания старается чаще использовать большие коробки. Если заказ составляет 96 банок, то как лучше упаковать его для отправки? Обычный подход
Эта задача имеет любопытное математическое решение. Если обозначить как x количество небольших коробок, а как y количество больших коробок, то мы получим уравнение: 8x + 10y = 96. В этом уравнении, однако, две неизвестные, что обычно означает наличие множества решений. Такое уравнение, где значения x и y могут быть только целыми, называют диофантовым по имени древнегреческого математика Диофанта (примерно 208–292 гг. н. э.). Попробуем решить его. Выразим x через y: 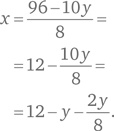
Значение члена
Образцовое решение
Для решения этой задачи лучше всего подходит стратегия учета всех возможностей и представление данных в табличной форме. 
Похоже, мы сразу получили один правильный ответ! Он удовлетворяет численным условиям задачи — необходимо отправить 96 банок. Вместе с тем единственная ли это возможность? В конце концов, такой ответ означает, что компания не использует ни одной большой коробки. А из условий нам известно, что она стремится использовать максимальное количество больших коробок. Поэтому продолжим таблицу и попробуем найти все возможные варианты. 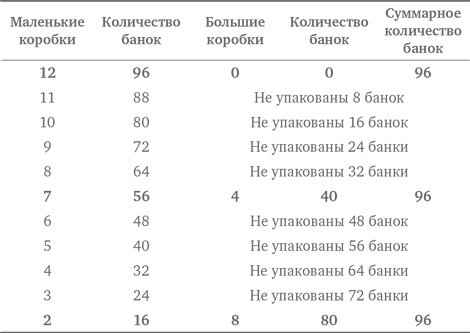
Существуют три варианта упаковки: 2 маленьких коробки и 8 больших; 7 маленьких коробок и 4 больших; 12 маленьких коробок и 0 больших. Вместе с тем, поскольку компания стремится использовать максимальное количество больших коробок, ответ для нашей задачи — 2 маленькие коробки и 8 больших. Обратите внимание на то, что с математической точки зрения все три ответа удовлетворяют условию, в соответствии с которым необходимо отправить 96 банок. Контекст задачи, однако, заставляет отбросить два варианта ответа из тех трех, что позволила выявить таблица. Задача 9.4
На стандартном игральном кубике точки на противоположных гранях составляют в сумме 7. Сколько разных сумм дают точки на трех соседних гранях стандартного кубика? Обычный подход
Одни обычно пытаются нарисовать кубик и последовательно подсчитать точки на соседних гранях. Другие начинают выписывать возможные сочетания точек на трех гранях, независимо от того, находятся они рядом или нет. Образцовое решение
Организуем данные таким образом, чтобы можно было учесть все возможности. Поскольку сумма точек на противоположных гранях равна 7, варианты сочетания могут быть лишь такими: 1 и 6; 2 и 5; 3 и 4. Известно, что у трех соседних граней должна быть общая вершина. Всего вершин у кубика восемь, поэтому наборов из трех соседних граней тоже должно быть восемь. Посмотрим, разные у них суммы точек или нет. Для этого перечислим все возможные сочетания по три, выбирая одно число на описанных выше трех парах противоположных граней, а потом определим их суммы. Чтобы не пропустить ни одной возможности, выбор будем проводить упорядоченно: 
Существует восемь разных сумм, как и следовало ожидать при восьми вершинах. Задача 9.5
Во время последней переписи населения респондент сказал переписчику, что у него трое детей. Когда его спросили об их возрасте, он ответил, что не может сказать этого, но произведение их возрастов равно 72, а сумма такая же, как номер нашего дома. Переписчик выбежал на улицу, посмотрел номер дома и сказал, что все равно не понимает. Тогда респондент добавил: «Ах да, я забыл сказать, что мой старшенький любит блинчики с черникой». После этого переписчик быстро заполнил графу возраста. Сколько лет детям респондента? (Рассматривайте только целые числа.) |
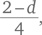 или d = 2–4k. Подставив это в приведенное выше уравнение, мы получаем q = 10 + k, а n = 20 — q — d = 20 — (10 + k) — (2–4k), или n = 8 + 3k.
или d = 2–4k. Подставив это в приведенное выше уравнение, мы получаем q = 10 + k, а n = 20 — q — d = 20 — (10 + k) — (2–4k), или n = 8 + 3k.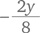 должно быть целым, чтобы получить целое значение x. Пусть y = 4. Тогда
должно быть целым, чтобы получить целое значение x. Пусть y = 4. Тогда
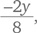 а x = 12 − 4–1 = 7. Таким образом, мы получаем семь маленьких коробок и четыре больших. Могут ли существовать другие ответы? Попробуем поискать их. Аналогичным образом можно принять y = 0 и получить 12 и 0. Наконец при y = 8 мы получаем x = 2.
а x = 12 − 4–1 = 7. Таким образом, мы получаем семь маленьких коробок и четыре больших. Могут ли существовать другие ответы? Попробуем поискать их. Аналогичным образом можно принять y = 0 и получить 12 и 0. Наконец при y = 8 мы получаем x = 2. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно