
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 40

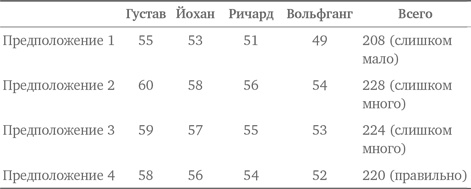
Таким образом, Густав пробежал свой этап за 58 секунд, Йохан — за 56 секунд, Ричард — за 54 секунды, Вольфганг — за 52 секунды. Задача 10.5
В коробке у Дэна находятся почтовые марки стоимостью 13 и 8 центов. Отправка посылки, которую он приготовил, стоит ровно $1. Сколько марок каждого достоинства Дэн должен наклеить на посылку? Обычный подход
Можно попробовать решить эту задачу алгебраически. Если обозначить как x количество 13-центовых марок и как y количество 8-центовых марок, то мы получим следующее уравнение: 0,13x + 0,08y = 1,00. Если перевести все в центы, то уравнение приобретет вид: 13x + 8y = 100. Это, однако, уравнение с двумя неизвестными, а значит ответов может быть несколько. Поскольку количество марок должно быть целым числом, нам нужно решить диофантово уравнение. Для начала выразим y через x:
Дробная часть должна быть целым числом, поскольку количество марок не может быть дробным. Выберем какое-нибудь значение для x, при котором дробная часть превращается в целое число. Пусть x = 4. Тогда y = 12 − 4 + (–2), или y = 6. Дэн, таким образом, должен использовать шесть 8-центовых марок и четыре 13-центовых марки. (Но все ли это возможности? Можно ли найти все возможные ответы?) Образцовое решение
Более изящное решение дает использование нашей стратегии обоснованного предположения и проверки в сочетании с табличным представлением результатов. 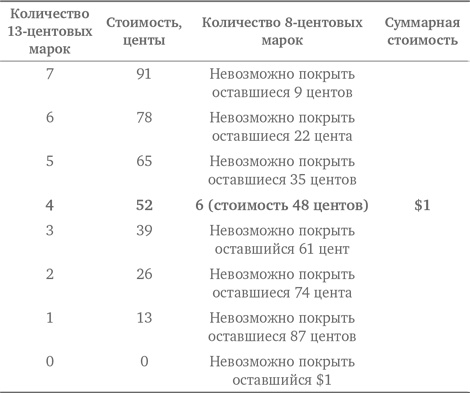
Таким образом, четыре 13-центовых марок и шесть 8-центовых марок дают сумму $1, необходимую Дэну. Обратите внимание на то, что таблица ясно показывает отсутствие других вариантов. Задача 10.6
Разница между двумя положительными целыми числами равна 5. Если сложить их квадратные корни, то сумма также будет равна 5. Что это за целые числа? Обычный подход
Традиционный подход — это составление системы уравнений: Пусть x = первое целое число; Пусть y = второе целое число. Тогда: 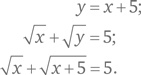
Возведем обе стороны в квадрат: 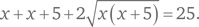
Упростим полученное выражение: 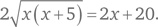
Снова возведем обе стороны в квадрат: 4x2 + 20x = 4x2 — 80x + 400; 100x = 400; x = 4; y = 9. Два целых числа — 4 и 9. Образцовое решение
Традиционный подход требует умения решать уравнения с радикалами и связан с большим количеством алгебраических преобразований. В качестве альтернативы воспользуемся нашей стратегией обоснованного предположения и проверки. Поскольку сумма квадратных корней из двух целых чисел равна 5, квадратные корни этих чисел должны представлять собой 4 и 1 или 3 и 2. Таким образом, целые числа должны быть равными 16 и 1 или 9 и 4. Вместе с тем, если взять разность, которая равна 5, становится понятно, что правильный ответ — 9 и 4. Задача 10.7
Тренер футбольной команды разрешает игрокам самостоятельно выбрать номер, под которым они выйдут на поле. Макс и Сэм, которые не только играют в футбол, но и входят в состав математической команды, останавливаются на особой паре номеров. Когда их номера возводят в квадрат, они дают двузначные числа. Когда два футболиста стоят рядом, образующееся из этих квадратов четырехзначное число также является квадратом простого числа. Какие номера они выбрали? Обычный подход
Большинство людей берут числа 1, 2, 3, 4, 5, … и возводят их в квадрат, пытаясь найти те, которые дают двузначный квадрат. Затем они помещают эти квадраты рядом друг с другом и смотрят, какие из них образуют квадрат простого числа. Такое гадание нельзя назвать продуктивным. Образцовое решение
Призовем на помощь нашу стратегию обоснованного предположения и проверки. Прежде всего, можно ограничить количество чисел, из которых делается выбор. При возведении в квадрат двузначное число дают числа от 4 до 9, поскольку квадраты 1, 2 и 3 — это однозначные числа, а квадраты 10, 11, …, 31 — трехзначные числа. Таким образом, мы можем выбирать из следующих квадратов: 16, 25, 36, 49, 64, 81. Начиная с 16 проверим, пара каких квадратов образует при размещении рядом квадрат простого числа. Обратите внимание, если мы оцениваем 1625 (это не квадрат простого числа), то нам нужно оценить и 2516 (тоже не квадрат простого числа). Чтобы выдвинуть обоснованное предположение, нужно в пару к 16 поставить оставшиеся двузначные числа. Если взять пару 16 и 81, то мы получим число 1681, равное 412. Макс и Сэм выбрали в качестве своих номеров числа 4 и 9. |
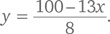 После деления и выделения целых величин и остаточных членов, а затем объединения остаточных членов мы получаем:
После деления и выделения целых величин и остаточных членов, а затем объединения остаточных членов мы получаем:
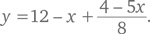
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно