Вселенная. Курс выживания среди черных дыр, временных парадоксов, квантовой неопределенности - читать онлайн книгу. Автор: Дэйв Голдберг, Джефф Бломквист cтр.№ 36

Самым простым на вид было бы действительно сложить циферблаты. Но прежде чем заняться этим, надо спросить себя, каковы, собственно, основания считать это действие правильным. Это хороший пример того, что в физике не все стоит считать само собой разумеющимся: проверка предположений часто ведет к новым идеям, как и в этом случае. Сделаем шаг назад и подумаем о чем-то как можно более общем – например, представим, что один циферблат переводится или сжимается (или расширяется) до общего сложения циферблатов. Рассмотрим эту возможность более подробно.

Мы говорим: «У меня есть два циферблата, и я хочу сочетать их, чтобы получился один, и я мог с его помощью узнать, какова вероятность нахождения двух электронов в точках А и В. Как мне их сочетать?» Не будем забегать вперед с ответом, потому что хотим понять, действительно ли стоит воспользоваться сложением циферблатов. Оказывается, мы не очень-то свободны в действиях, и, как ни странно, простое сложение циферблатов – это одна из всего двух возможностей.

Чтобы упростить разговор, будем называть циферблат, соответствующий движению частицы 1 в точку А и движению частицы 2 в точку В, циферблатом 1. Это циферблат, который связан с верхней иллюстрацией на рис. 7.3. Циферблат 2 соответствует другой возможности, когда частица 1 приходит в точку В. Важно понять: если мы переведем циферблат 1 до сложения с циферблатом 2, то вычисляемая общая вероятность должна быть такой же, как если бы мы таким же образом перевели циферблат 2 перед его сложением с циферблатом 1.

В доказательство этого можно указать, что перемена наименований А и В в наших диаграммах, очевидно, не может ничего изменить. Это просто иной способ описания одного и того же процесса. Но если поменять А на В и наоборот, то и диаграммы на рис. 7.3 поменяются местами. Это значит, что, если мы решим подкрутить циферблат 1 (соответствующий верхней диаграмме) перед его прибавлением к циферблату 2, это действие должно полностью соответствовать смещению циферблата 2 перед его прибавлением к циферблату 1 после того, как мы поменяли их названия. Это логическое соображение жизненно важно для нас, так что его необходимо довести до сознания. Так как мы предположили, что нет возможности определить разницу между двумя частицами, то можно поменять местами их названия. Это значит, что подведение циферблата 1 должно давать тот же результат, что и такое же подведение циферблата 2, поскольку нет никакой возможности эти циферблаты различить.

Приведенное выше наблюдение нельзя назвать скромным или незначительным: оно имеет очень важные последствия, поскольку существует лишь два возможных способа подведения и уменьшения циферблатов, прежде чем сложить их, в результате чего получится конечный циферблат со свойствами, не зависящими от того, какой из исходных циферблатов подвергся обработке. Это показано на рис. 7.4. Верхняя половина рисунка иллюстрирует, что если подкрутить циферблат 1 на 90° и прибавить его к циферблату 2, то получившийся циферблат будет не равен по размеру тому, который получится, если подкрутить на 90° циферблат 2 и прибавить его к циферблату 1. Это можно видеть, потому что, если сначала подкрутить циферблат 1, то новая стрелка, которая показана здесь пунктиром, будет показывать в противоположном по отношению к стрелке циферблата 2 направлении, таким образом частично отменяя этот циферблат. При смещении же циферблата 2 его стрелка продолжает указывать в том же направлении, что и стрелка циферблата 1, так что они прибавляются, образуя более длинную стрелку.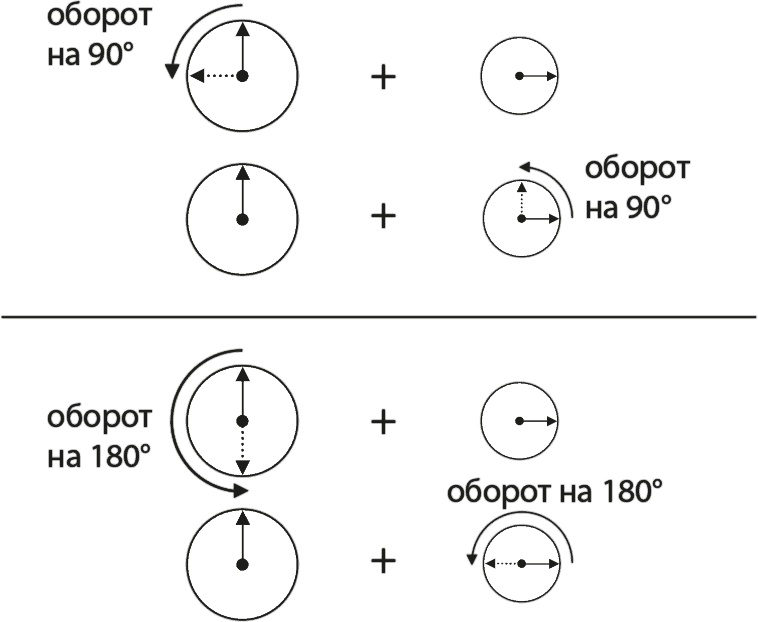

Рис. 7.4. Верхняя часть рисунка показывает, что сложение циферблатов 1 и 2 после смещения циферблата 1 на 90° не эквивалентно их сложению после смещения на те же 90° циферблата 2. Нижняя часть показывает интересную возможность смещения одного из циферблатов на 180° перед сложением

Должно быть ясно, что 90° – это не какой-то особый случай, и другие углы тоже дадут циферблаты, которые зависят от того, который из двух исходных мы предпочли подкрутить.

Очевидное исключение – это перевод стрелки часов на 0°, потому что смещение циферблата 1 на 0° с последующим его сложением с циферблатом 2 – это, разумеется, то же самое, что и смещение циферблата 2 на 0° с последующим его сложением с циферблатом 1. Это значит, что сложение циферблатов без всякого перевода их стрелок – это вполне жизнеспособная возможность. Точно так же подойдет и подведение обоих циферблатов на одну и ту же величину, но это фактически та же ситуация, что и случай «без смещения»: нужно просто переопределить то, что мы будем называть «12 часами». Это равноценно утверждению, что мы всегда можем смещать любой циферблат на определенную величину, если эта величина равна для всех циферблатов. Это никогда не будет оказывать воздействие на те вероятности, которые мы пытаемся подсчитать.

Нижняя часть рис. 7.4 показывает, что, как бы странно это ни звучало, есть еще один способ сочетания циферблатов: мы можем повернуть один из них на 180° с последующим их сложением. Не получается один и тот же циферблат в двух случаях, но размер при этом остается тем же самым, следовательно, это приводит к той же самой вероятности нахождения одного электрона в точке А и другого в точке В.

Подобные рассуждения можно привести и по поводу возможности сжатия или расширения одного из циферблатов перед их сложением, потому что если мы сожмем циферблат 1 на определенную величину, прежде чем прибавить его к циферблату 2, то получаться будет не тот результат, что при сжатии циферблата 2 на ту же величину перед сложением его с циферблатом 1, и исключений у этого правила нет.

Итак, можно сделать интересный вывод. Хотя мы начали с того, что даровали себе полную свободу действий, оказалось, что, поскольку нет возможности отличить частицы друг от друга, есть лишь два способа сочетания циферблатов: мы можем сложить их либо сразу, либо после поворота стрелки одного из них на 180°. И самое замечательное, что природа идет обоими путями.

В случае с электронами перед сложением циферблатов нужно произвести лишний оборот. В случае с фотонами или бозонами Хиггса нужно сложить циферблаты, не прибегая к повороту. Итак, частицы природы делятся на два типа: те, которым нужен лишний оборот, называются фермионами, а те, которые обходятся без него, именуются бозонами.

Что определяет, фермион конкретная частица или бозон? Ее спин. Спин, как можно догадаться по этимологии слова (от англ. spin – «вращать»), – это мера углового момента частицы, и фермионы всегда имеют спин, равный полуцелому числу ^[34], а у бозонов спин целый. Мы говорим, что у электрона спин равен ½, у фотона – 1, а у бозона Хиггса – 0. Не хотим вдаваться в подробности по поводу спина, потому что они в основном чисто технические. Однако в разговоре о периодической системе оказалось важно, что в результате электроны делятся на два типа в соответствии с двумя возможными значениями их углового момента (спин, направленный вверх, или спин, направленный вниз). Это пример общего правила, которое гласит: частицы со спином s обычно имеют 2s + 1 типов, например частицы со спином ½ (то есть электроны) имеют два типа, со спином 1 – три типа, а со спином 0 – один тип.