Вселенная. Курс выживания среди черных дыр, временных парадоксов, квантовой неопределенности - читать онлайн книгу. Автор: Дэйв Голдберг, Джефф Бломквист cтр.№ 35

В оставшейся части этой главы мы попытаемся объяснить, почему электроны ведут себя столь странным образом, описанным в принципе Паули. Как обычно, постараемся по максимуму использовать наши квантовые циферблаты. Для этого подумаем, что произойдет при «отталкивании» электронов друг от друга. На рис. 7.3 показан конкретный сценарий, когда два электрона, помеченные цифрами 1 и 2, начинают свое движение в одном месте и заканчивают в каком-то другом. Конечные точки мы отметили буквами А и В. Заштрихованные круги напоминают, что мы пока не думали по поводу того, что случается при взаимодействии двух электронов друг с другом (подробности этого процесса для нынешних целей не имеют особого значения).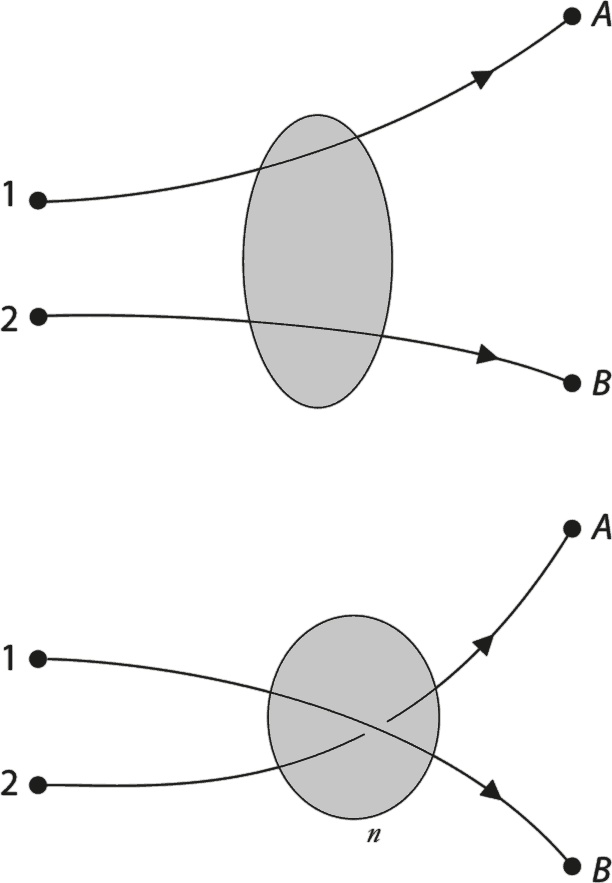

Рис. 7.3. Разлет двух электронов

Нужно представить, что электрон 1 выпрыгивает из исходной точки и заканчивает движение в точке А. Точно так же электрон 2 «приземляется» в точке В. Это показано на верхней иллюстрации. На самом деле аргумент, который мы намерены предъявить, прекрасно работает, даже если игнорировать возможность взаимодействия электронов. В этом случае электрон 1 попадает в точку А независимо от любых блужданий электрона 2, и вероятность найти электрон 1 в точке А и электрон 2 в точке В будет всего лишь произведением двух независимых вероятностей.

Например, представим, что вероятность прибытия электрона 1 в точку А равна 45 %, а вероятность электрона 2 в точку В – 20 %. Вероятность нахождения электрона 1 в точке А и электрона 2 в точке В равна 0,45 × 0,2 = 0,09 = 9 %. Здесь мы пользуемся обычной логикой, которая говорит, что вероятность подбросить монетку, чтобы выпал орел, и вместе с тем бросить кубик, чтобы выпала шестерка, равны ½ × ⅙, что составляет 1/12 (то есть чуть больше 8 %) ^[33]. Как показано на иллюстрации, у электронов есть и другой способ оказаться в точках А и В. Электрон 1 может попасть в точку В, а электрон 2 – в точку А. Допустим, вероятность найти электрон 1 в точке В равна 5 %, а вероятность найти электрон 2 в точке А – 20 %. Тогда вероятность найти электрон 1 в точке В и электрон 2 в точке А равна 0,05 × 0,2 = 0,01 = 1 %.

Таким образом, у нас есть два варианта нахождения двух электронов в точках А и В – один с вероятностью 9 % и один с вероятностью 1 %. Таким образом, вероятность того, что один электрон будет в точке А, а другой в точке В, если не имеет значения, какой где окажется, должна составлять 9 % + 1 % = 10 %. Все просто; но неверно.

Ошибка состоит в предположении о том, что вообще можно утверждать, какой электрон попадает в точку А, а какой в точку В. Что если электроны полностью идентичны? Кажется, что этот вопрос не имеет никакого значения, однако это не так. Кстати, предположение, что квантовые частицы могут быть полностью идентичны, впервые было сформулировано в связи с законом излучения черного тела Планка. Малоизвестный физик Ладислас Натансон еще в 1911 году заметил, что закон Планка несовместим с предположением, что фотоны можно идентифицировать. Иными словами, если бы можно было пометить фотон и отследить его передвижения, закон Планка не получился бы.

Если электроны 1 и 2 совершенно идентичны, можно описать процесс их разлета следующим образом: изначально есть два электрона, а еще через некоторое время по-прежнему есть два электрона, расположенных в разных местах. Как нам уже известно, квантовые частицы не двигаются по хорошо определенным траекториям, так что даже в принципе невозможно отследить их перемещение. Таким образом, нет смысла утверждать, что электрон 1 появился в точке А, а электрон 2 – в точке В. Мы просто не можем этого сказать, а стало быть, нет смысла их как-то маркировать. Вот что понимается под «идентичностью» частиц в квантовой теории. И куда же нас заведут подобные рассуждения?

Посмотрите еще раз на рисунок. В нашем конкретном случае две вероятности, которые мы связывали с двумя диаграммами (9 % и 1 %), верны. Однако это еще не все. Мы знаем, что квантовые частицы описываются циферблатами, так что мы должны связать циферблат с электроном 1, прибывающим в точку А, при этом размер циферблата будет равен √45 %. Точно так же другой циферблат будет связан с электроном 2, прибывающим в точку В, и его размер будет равняться √20 %. Теперь можно сформулировать новое квантовое правило: оно гласит, что мы должны связать отдельный циферблат с целым процессом, то есть будет существовать циферблат с размером, квадрат которого будет равен вероятности нахождения электрона 1 в точке А и электрона 2 в точке В. Иными словами, верхней иллюстрации на рис. 7.3 будет соответствовать свой циферблат. Мы видим, что этот циферблат должен иметь размер, равный √9 %, поскольку именно с этой вероятностью происходит процесс. Но какое время он будет показывать? Ответ на этот вопрос будет дан в главе 10, и он связан с идеей умножения циферблатов. Для целей же этой главы знать время необязательно; понадобится лишь только что сформулированное новое важное правило, которое стоит даже повторить, потому что оно существенно для всей квантовой теории: мы должны связать одиночный циферблат со всеми возможными способами, которыми может идти весь процесс. Циферблат, который мы связываем с нахождением одиночной частицы в конкретном месте, – это простейшая иллюстрация нашего правила, и до этого места в книге мы уже продвинулись. Но это особый случай, и раз уж мы начали рассматривать более одной частицы, то правило нуждается в расширении. Это значит, что с верхней иллюстрацией на рисунке связан циферблат размером 0,3. Точно так же есть и второй циферблат размером 0,1 (потому что 0,12 – это 0,01, то есть 1 %), связанный с нижней иллюстрацией на рисунке. Таким образом, у нас есть два циферблата, и нужно найти способ использовать их для определения вероятности найти один электрон в точке А и другой в точке В. Если бы эти два электрона можно было отличить друг от друга, ответ был бы очевидным: мы просто сложили бы вероятности (но не циферблаты), связанные с каждой возможностью. У нас получился бы ответ – 10 %.

Но если нет никакого способа определить, какой из изображенных на диаграммах процессов произошел в действительности – что справедливо, если электроны неотличимы друг от друга, – то, следуя логике, которую мы разработали для скачков одиночной частицы из точки в точку, нужно складывать именно циферблаты. Мы стоим на пороге обобщения правила, утверждающего, что для одной частицы нужно складывать циферблаты, связанные со всеми различными способами достижения этой частицей определенной точки, чтобы определить вероятность нахождения частицы в этой конкретной точке. Для системы, состоящей из множества идентичных частиц, нужно сочетать все циферблаты, связанные со всеми возможными способами, которыми эти частицы могут попасть в свои конечные пункты, чтобы определить вероятность их нахождения в этих конечных пунктах. Это достаточно важное положение, чтобы перечитать его несколько раз: должно быть ясно, что этот новый закон сочетания циферблатов служит обобщением закона, который мы использовали для одиночной частицы. Однако вы могли заметить, что мы очень тщательно выбираем термины. Мы не сказали, что циферблаты нужно обязательно складывать: мы говорим, что их нужно сочетать. И для такой оговорки есть причины.