Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний - читать онлайн книгу. Автор: Джеффри Уэст cтр.№ 134

Это видно из рис. 78, на котором черные точки, обозначающие начало каждого следующего цикла инновации, со временем становятся все ближе друг к другу: по мере того как мы поднимаемся все выше по каждой кривой роста, ускоряется не только темп жизни, но и появление крупных инноваций и переходы в новое состояние должны происходить со все более высокой скоростью. Метафора беговой дорожки, которую я использовал в главах 1 и 8, когда говорил о сжатии социально-экономического времени и увеличении темпа жизни, раскрывает лишь часть ситуации, и здесь имеет смысл поговорить о ней более подробно. Мы не только живем на ускоряющейся беговой дорожке, которая все время движется все быстрее и быстрее, но должны в какой-то момент перепрыгнуть на другую дорожку, движущуюся с еще большим ускорением, а затем с той – на следующую, еще более быструю. И этот процесс неизбежно будет повторяться в будущем со все более высокой частотой.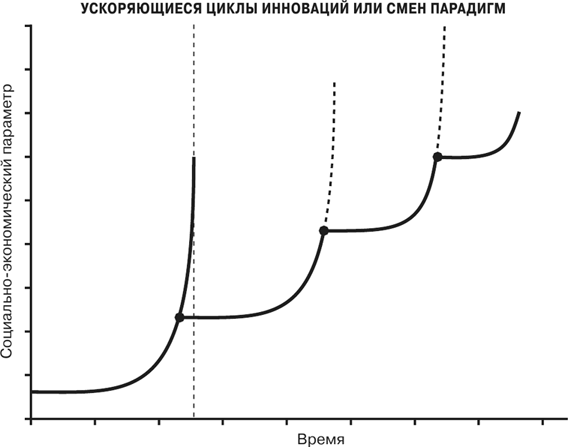

Рис. 78. График последовательных траекторий суперэкспоненциального роста, каждая из которых может привести к сингулярности конечного времени (обозначенной вертикальной штриховой линией) и последующему краху, как на рис. 77, если до наступления сингулярностей не появляются инновации (обозначенные черными точками), обнуляющие отсчет времени и начинающие новый цикл. Для ясности представления штриховые линии, обозначающие позднейшие сингулярности конечного времени, соответствующие черным точкам, не показаны. Слева изображен Сизиф

В этой поразительной картине есть нечто странное и даже безумное. Трудно поверить, чтобы человечество могло продолжать такое существование, не получив коллективного инфаркта! Сизифов труд выглядит по сравнению с ним вполне легкой работой. Вы, наверное, помните, что боги обрекли Сизифа беспрестанно закатывать большой камень на вершину горы, с которой он немедленно скатывается вниз под действием собственного веса, и Сизиф должен заново начинать свой путь с самого низа. Рассказывают о множестве разных поступков, за которые Сизиф был так жестоко наказан, но мне особенно нравятся два из них, родственные тому сизифову труду, который мы создали сами для себя: говорят, что он украл тайны богов и заковал в цепи Смерть. Остается только сказать, что наша задача на самом деле много труднее той, что досталась Сизифу: мы должны не просто снова и снова закатывать камень на вершину горы, но делать это каждый раз все быстрее и быстрее.

Существование таких теоретически предсказанных последовательных и ускоряющихся циклов роста, скорость которого превышает экспоненциальную, подтверждается наблюдениями развития городов, волн технологических изменений и численности мирового населения (я уже упоминал работу Сорнета и Йохансена). Посмотрим, например, на кривую роста города Нью-Йорка с 1790 г. до наших дней, представленную на рис. 58 в главе 8. Последовательные фазы его роста выделены жирными черными линиями. При рассмотрении их отклонений от гладкой фоновой кривой «чистого» суперэкспоненциального роста ясно проявляется последовательность изменений, отражающая циклическую динамику изменений размеров города. Как видно из рис. 79, данные подтверждают предположение о том, что частота смены циклов систематически возрастает со временем. На врезке показано, что промежутки времени между такими последовательными «инновациями» все более сокращаются в численном согласии с предсказаниями теории.

Предсказание об ускорении циклов крупных инноваций так же убедительно подтверждается данными и на более крупном масштабе. Одна из трудностей рассмотрения этого вопроса связана с выбором из огромного числа произошедших инноваций тех, которые могут представлять собой крупные смены парадигмы. В некоторой степени этот выбор остается субъективным, но, вероятно, большинство из нас согласится с тем, что некоторые открытия и изобретения – например, книгопечатание, использование угля, телефон или компьютер – это крупные «смены парадигмы», а вот насчет железной дороги или персонального компьютера можно и поспорить. К сожалению, развитой численной «теории инноваций» не существует, а потому не существует и общепризнанных критериев или данных, непосредственно относящихся к крупным инновациям и сменам парадигмы. Таким образом, чтобы сравнить теорию с данными, нам приходится полагаться на неформальные исследования и, до некоторой степени, на интуицию. Это положение вполне может измениться, так как инновации становятся предметом все более активного изучения, и исследователи пытаются определить, что такое инновации, как их можно измерить, как они происходят и как мы можем их стимулировать ^[169].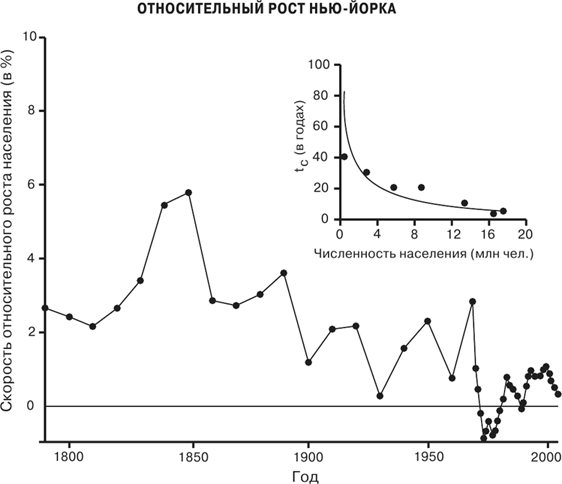

Рис. 79. Отклонения роста Нью-Йорка с 1790 г. от суперэкспоненциального фона, демонстрирующие последовательные циклы, частота которых систематически уменьшается в количественном согласии с теоретическими предсказаниями (кривая на врезке)

Известный изобретатель и футуролог Рэй Курцвейл составил и проанализировал список кандидатур на роль крупных инноваций в формате, весьма подходящем для сравнения с нашими предсказаниями ^[170]. Его результаты показаны на рис. 80 и 81, на которых построена зависимость времени, проходящего между двумя последовательными инновациями, от удаленности каждой из инноваций в прошлое. На рисунках представлены два варианта одного и того же графика, в полулогарифмическом масштабе (то есть с логарифмическим масштабом по вертикальной оси и линейным по горизонтальной) и в логарифмическом масштабе по обеим осям. Чтобы сориентироваться в этих графиках, отметим, что первая точка в левом верхнем углу обоих рисунков обозначает возникновение жизни, случившееся около 4 × 10⁹ (четырех миллиардов) лет назад, – это число отложено по горизонтальной оси; а следующая крупная инновация произошла лишь почти два миллиарда лет спустя – и это число отложено по вертикальной оси. Интересно отметить, что в линейном временном масштабе (на рис. 80) кажется, что все события после появления самых ранних предков человека, что случилось около миллиона лет назад, произошли одновременно. Кривая резко падает, наглядно иллюстрируя ускорение времен. Из этого графика также видно, почему применение логарифмического масштаба (рис. 81) для отображения таких данных гораздо информативнее, так как позволяет разделить события, происходящие по всей этой гигантской временной шкале. Например, при таком отображении изобретение телефона, случившееся всего сотню лет назад, можно отделить во времени от появления сельского хозяйства, произошедшего целых десять тысяч лет назад.