Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний | Джеффри Уэст | страница 135 | LoveRead.ec

Теория объясняет и предсказывает такое обратное соотношение между последовательным сокращением интервалов между инновациями и временем, отделяющим их от нас, и количественно согласуется с линиями, проведенными на обоих графиках. Поспешу отметить, однако, что предсказания относятся лишь к той части графиков, которая касается инноваций, связанных с социально-экономической динамикой, которая порождает человеческую изобретательность; теория ничего не говорит о скорости возникновения инноваций биологических. Это оставляет без ответа следующий интересный вопрос: играет ли аналогичная динамика сингулярностей сходную роль в отношении биологических инноваций, или же наблюдаемое согласие и продолжение зависимости по простому степенному закону в область самого раннего времени, предшествующего появлению человека, – всего лишь случайность или результат предвзятого выбора смен парадигм Курцвейлом? Во всяком случае, согласие данных с теорией в области ее применимости выглядит убедительно и подтверждается более подробным анализом периода, ограниченного несколькими последними столетиями.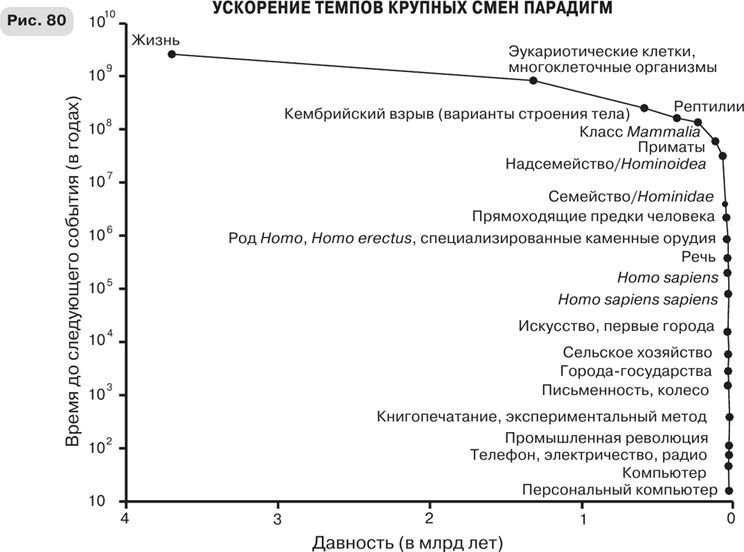

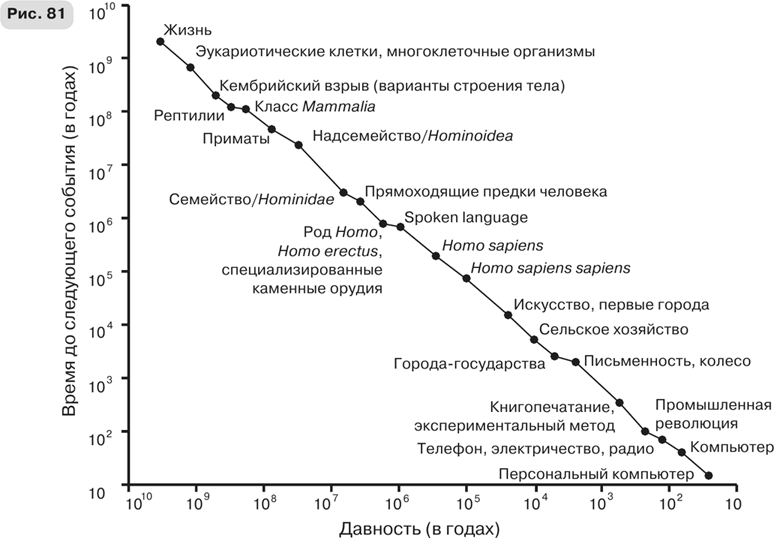
Зависимость временных интервалов между крупными инновациями от их давности, представленная в полулогарифмическом (рис. 80) и логарифмическом (рис. 81) масштабах

Общая концепция сингулярности играет важную роль в математике и теоретической физике. Сингулярностью называют точку, в которой математическая функция неким определенным образом перестает «хорошо себя вести», например становится бесконечной так, как было описано выше. Обсуждение возможностей укрощения таких сингулярностей привело к огромному прогрессу математики XIX в., и это впоследствии оказало большое влияние на теоретическую физику. Наиболее знаменитым следствием изучения сингулярностей стала концепция черных дыр, возникшая из попыток понять структуру сингулярностей общей теории относительности Эйнштейна.

До того как слово «сингулярность» было популяризовано Курцвейлом в опубликованной в 2005 г. книге «Сингулярность уже близка: когда люди выйдут за пределы биологии» (The Singularity Is Near: When Humans Transcend Biology), этот термин почти не употреблялся в обиходной речи. Развивая более раннюю идею «технологической сингулярности», предложенную в 1993 г. писателем-фантастом и специалистом по информатике Вернором Винджем, Курцвейл утверждал, что мы приближаемся к сингулярности, в которой наши тела и мозги будут усовершенствованы при помощи генетических изменений, нанотехнологий и искусственного интеллекта, и мы превратимся в гибридных киборгов, уже не ограниченных рамками биологии. Предполагалось, что это приведет к возникновению коллективного разума, неизмеримо более мощного, чем разум всех ныне существующих людей, вместе взятых. Или, как лаконично сформулировал эту идею Виндж: «В течение тридцати лет мы получим технические средства для создания сверхчеловеческого разума. Вскоре после этого эра человечества закончится»^[171]. Так как это было написано в 1993 г., предсказание утверждает, что такое должно произойти к 2023 г., до которого осталось всего семь лет. Я так не думаю.

Возможно, эти увлекательные предположения когда-нибудь и осуществятся, но пока что они принадлежат к области научной фантастики. Хотя такое радужное видение будущего почти диаметрально противоположно мрачным прогнозам неомальтузианцев, забавно отметить, что выводы в обоих случаях основываются на одной и той же предпосылке неустойчивости экспоненциального роста и неизбежности каких-то резких изменений. Если мальтузианцы упускали из виду принципиально важную роль инноваций, то провозвестники сингулярности точно так же не учитывают принципиально важную роль всей социально-экономической динамики нашей планеты, которая на самом деле и является движущей силой приближающейся сингулярности. Поскольку ни те ни другие не опираются на более общую систему, которая включала бы в себя численную механистическую теорию, их предсказания, каковы бы они ни были, трудно оценить с научной точки зрения. Возможно, наибольшая концептуальная ирония, особенно в отношении сингуляристов, заключается в том, что их выводы и предположения основаны на принципе экспоненциального роста, который, собственно говоря, не порождает никакой сингулярности, во всяком случае в течение конечного времени.

Тем не менее экспоненциальный рост вполне может быть неустойчивым, и именно по тем самым конкретным причинам, которые выдвигал изначально Мальтус: мы можем оказаться не в состоянии производить достаточно пищи или энергии или столкнуться с нехваткой каких-нибудь существенных ресурсов – например, фосфора, нефти или титана – и в то же время не суметь разработать соответствующие технологии, которые позволили бы устранить эту проблему. Кроме того, мы можем произвести такое количество энтропии, что вызванные нашей деятельностью загрязнение окружающей среды, экологический ущерб и другие разрушительные побочные эффекты, в особенности те, которые влияют на климат, приведут к невообразимым опустошительным последствиям. Напомню, однако, что если это произойдет в результате экспоненциального роста, то в принципе ничто не помешает нам прийти к тем достижениям, близость которых провозглашают оптимисты, и продолжить свой рост, избавляясь от всех этих многочисленных проблем и угроз при помощи инноваций. Но на практике дело может обстоять совсем по-другому, и я вовсе не уверен, что мы сможем этого добиться.

Однако в реальности ситуация иная, причем иная качественно. Как я подчеркивал выше, под воздействием суперлинейного масштабирования социально-экономической деятельности, порожденного мультипликативным усилением, присущим нашей социальной динамике, мы расширяемся не «просто» экспоненциально, но суперэкспоненциально. Эта неотъемлемо свойственная современному человечеству динамика приводит к увеличению темпа жизни и той скорости, с которой мы должны производить крупные инновации, чтобы преодолеть надвигающуюся угрозу сингулярностей конечного времени. Нас преследует образ ускоряющегося Сизифа.

Между «компьютерным веком» и «информационно-цифровым веком» прошло не более тридцати лет – в то время как века каменный, бронзовый и железный разделяли тысячелетия. Время, которое мы отсчитываем по своим часам или электронным устройствам, очень обманчиво: оно определяется суточным вращением Земли вокруг собственной оси и ее же годовым обращением вокруг Солнца. Астрономическое время линейно и регулярно. Но те часы, по которым мы проживаем свою социально-экономическую жизнь, – это эмерджентное явление, определяемое коллективными силами социальных взаимодействий: они непрерывно и систематически ускоряются по сравнению с объективным астрономическим временем. Мы живем на все той же пресловутой социально-экономической беговой дорожке, движущейся с ускорением. Крупная инновация, на возникновение которой тысячу лет назад или еще раньше могли уйти столетия, сейчас может появиться всего за тридцать лет. Вскоре этот срок сократится до двадцати пяти, затем до двадцати, семнадцати и так далее – и, подобно Сизифу, мы обречены снова и снова повторять все сначала, если мы собираемся продолжать непрерывно расти и расширяться. Получающаяся в результате этого процесса последовательность сингулярностей, каждая из которых грозит нам застоем и крахом, будет продолжать накапливаться, стремясь к тому, что математики называют существенной сингулярностью, своего рода прародительнице всех сингулярностей.