Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний | Джеффри Уэст | страница 113 | LoveRead.ec

Как я уже объяснял, данные сотовой телефонии дают подробную информацию не только о том, с кем и как долго вы разговаривали, но и о том, когда это происходило и где вы при этом находились. По сути дела, каждый из нас носит с собой прибор, отслеживающий, где мы находимся в любой момент. Как если бы мы могли пометить каждую из молекул, находящихся в комнате, и отслеживать таким образом ее положение, скорость ее движения, с чем она сталкивается и так далее. Поскольку в комнате обычных размеров находится более десяти тысяч триллионов триллионов (10²⁸) молекул, мы получили бы при этом настоящую квинтэссенцию «больших данных». Однако вся эта информация была бы на самом деле не очень полезной, особенно в отношении газов, находящихся в равновесном состоянии: такое исследование было бы избыточным. В статистической физике и термодинамике уже успешно разработаны мощные методы, позволяющие понять и описать макроскопические свойства газов – например, их температуру, давление, фазовые переходы и так далее, – не вдаваясь в неприглядные подробности движения всех составляющих их молекул. Напротив, в случае городов такая информация чрезвычайно ценна, не только потому, что молекулами здесь являемся мы сами, но и потому, что, в отличие от газов, города представляют собой сложные адаптивные системы со сложнейшими сетевыми структурами, осуществляющими обмен как энергией, так и информацией. Данные мобильной телефонии дают нам мощный инструмент для определения структуры и динамики этих сетей и, следовательно, для количественной проверки теоретических предсказаний.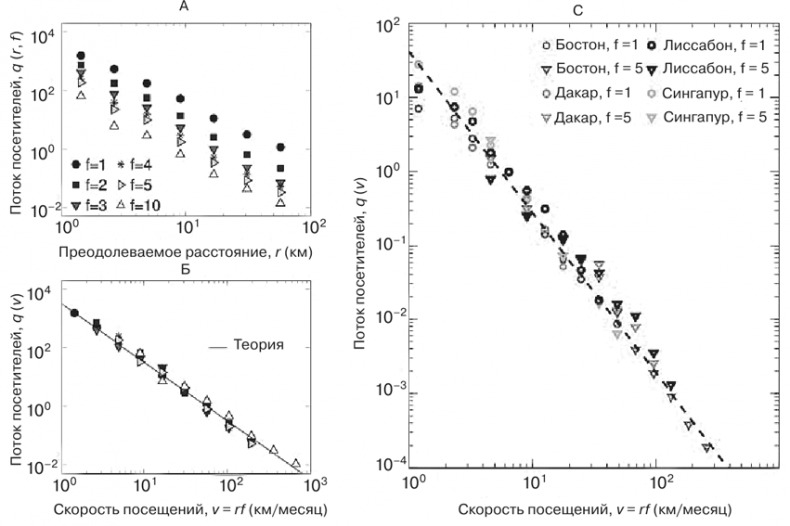

Рис. 47. а) Поток посетителей конкретного района Бостона, приезжающих с разных расстояний с разной, но постоянной частотой (f раз в месяц), демонстрирует согласие с законом обратных квадратов. б) Те же данные, что и на графике «а», иллюстрирующие сведение всех частот и расстояний в единую линию при построении зависимости от единой переменной, произведения частоты на расстояние. в) График, аналогичный графику «б», демонстрирующий, что поток посетителей в самых разных городах всего мира подчиняется одному и тому же предсказанному закону обратных квадратов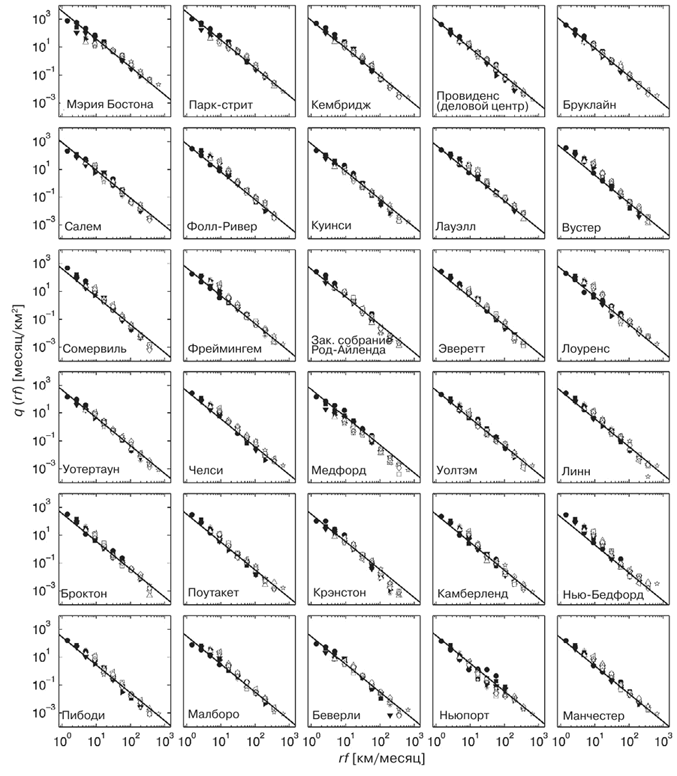

Рис. 48. График, аналогичный графику «в», для разных районов Бостона

Рис. 49. То же для разных районов Сингапура; сплошной линией представлены предсказания теории

Эта закономерность может стать мощным инструментом планирования и развития городов, поскольку она дает основу для оценки потоков людей в определенные районы города и из них. Строительство нового торгового центра или жилого микрорайона требует точной – или по меньшей мере правдоподобной – оценки транспортных и человеческих потоков для организации действенной и достаточной транспортной системы. Такие оценки по большей части получают из компьютерных моделей, несомненно очень полезных, но в основном сильно локализованных, не учитывающих взаимоотношений с большей, интегрированной системной динамикой города и очень редко основанных на общих фундаментальных принципах.

Блестящий анализ огромных объемов данных мобильной телефонии, использованных для проверки нашей теории, провели швейцарский инженер Маркус Шлепфер и венгерский физик Майкл Селл, два представителя группы талантливых постдокторантов, которых Карло Ратти завербовал в MIT. Впоследствии, в 2013 г., Маркус присоединился к нам в Институте Санта-Фе, в котором мы начинали эту работу. Один из особенно интересных его проектов, над которым он работал вместе с Луисом, касался анализа соотношения высот и объемов зданий с размерами города. С тех пор Маркус перешел в престижную Высшую техническую школу (ЕТН) своего родного Цюриха и участвует там в большом совместном проекте под названием «Лаборатория городов будущего» (Future Cities Lab), который базируется в Сингапуре и получает поддержку правительства этой страны.

8. Перевыполнение и недовыполнение

Большинство из нас очень интересуется рейтингами, будь то рейтинги городов, школ, университетов, корпораций, штатов или стран, не говоря уже о футбольных командах или теннисистах. В основе рейтингов, разумеется, лежит выбор параметров и методик, по которым их составляют. То, как именно задаются вопросы и какой сегмент населения выбирают для опроса, может сильно влиять на результаты опросов и анкет, что может приводить к серьезным последствиям в политике и бизнесе. Такие рейтинги играют все более важную роль в принятии решений – как частными лицами, так и планировщиками и идеологами в государственных органах и промышленности. Рейтинг города или штата по уровню здоровья населения, образования, налогообложения, занятости или преступности, в масштабах всего мира или данной страны, может оказывать сильное влияние на его образ в глазах инвесторов, крупных компаний или туристов.

В спорте бесконечно обсуждается вопрос о величайших игроках или командах в истории: вопрос, очевидно не имеющий сколько-нибудь объективного ответа. Проблема заключается не только в выборе параметров и разумных критериев «величия», но и в том, что речь обычно идет о сравнении несравнимых вещей («яблок с апельсинами»), да зачастую еще и за разные исторические периоды. В связи с этим мы можем ненадолго вернуться к обсуждению результатов в тяжелой атлетике, о которых мы говорили в главе 2, и вспомнить эпохальное открытие Галилея, согласно которому сила конечностей животного должна масштабироваться сублинейно, пропорционально массе тела в степени ⅔. Это предсказание подтверждается результатами тяжелоатлетов, представленными на рис. 7. Я предложил тогда рассматривать кривую масштабирования в качестве стандарта, относительно которого следует измерять результаты спортсменов: она показывает, какой вес должен поднимать идеализированный чемпион по тяжелой атлетике, имеющий ту или иную собственную массу. Степенной закон масштабирования с показателем ¾, представленный на рис. 1, точно так же показывает, каким «должен» быть уровень метаболизма идеализированного организма тех или иных размеров. «Идеализированной» следует в этом случае считать систему, «оптимизированную» с точки зрения энергопотребления, динамики и геометрии сетевых структур, как было объяснено в главе 3.

Эта концепция была использована в качестве отправной точки для разработки научной меры результативности. Четверо из наших шести чемпионов подняли тот вес, который они и должны были поднять по прогнозам закона масштабирования. Вместе с тем спортсмен среднего веса перевыполнил предполагаемую для своих размеров норму, а тяжеловес недовыполнил свою. Поэтому, хотя тяжеловес поднял больший вес, чем кто бы то ни было, с научной точки зрения он оказался самым слабым из всех чемпионов, а спортсмен, выступавший в среднем весе, – самым сильным.