
|
||
|
|
||
|
|
Онлайн книга - Опасная идея Дарвина: Эволюция и смысл жизни | Автор книги - Дэниел К. Деннетт
Cтраница 156

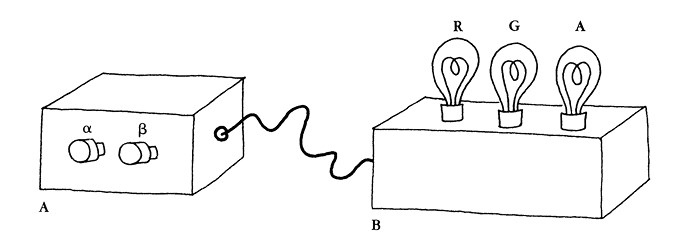
Ил. 42 2. Два черных ящика
746
Давным-давно жили-были два больших черных ящика, A и B, соединенные длинным изолированным медным проводом. На ящике A было две кнопки, помеченные буквами α и β, а на ящике B – три лампочки: красная, зеленая и янтарно-желтая. Согласно наблюдениям ученых, изучавших поведение ящиков, каждый раз, когда вы нажимали кнопку α на ящике A, на ящике B вспыхивала красная лампочка, а каждый раз, когда вы нажимали кнопку β на ящике A, вспыхивала лампочка зеленая. Складывалось впечатление, что янтарно-желтая лампочка никогда не загорается. Ученые провели миллиард экспериментов в весьма разнообразных условиях и обнаружили, что из этого правила нет исключений. Им казалось, что существует каузальная закономерность, которую они для наглядности резюмировали так: Все α приводят к красному. Все β приводят к зеленому. Они определили, что каузальная связь каким-то образом устанавливается с помощью медного провода, поскольку, когда они его перерезали, лампочки на ящике B перестали загораться, а при попытках загородить ящики друг от друга, не перерезая провод, закономерность никогда не нарушалась. Поэтому им, естественно, было интересно узнать, каким образом открытая ими каузальная закономерность осуществлялась с помощью провода. Возможно – думали они – нажатие кнопки α вызывает низковольтный разряд, который проходит по проводу и заставляет срабатывать красную лампочку, а нажатие кнопки β вызывает высоковольтный разряд, который заставляет вспыхивать зеленую лампочку. Или, может быть, нажатие кнопки α вызывает единичный разряд, зажигающий красную лампочку, а нажатие кнопки β – двойной разряд. Ясно, что нечто всегда возникало в проводе при нажатии кнопки α, а нечто другое всегда возникало при нажатии кнопки β. Если бы они обнаружили, что бы это могло быть, то объяснили бы открытую ими каузальную закономерность. Своего рода прослушивание провода вскоре показало, что все сложнее. Какая бы кнопка ни нажималась на ящике A, по проводу в ящик B тут же пересылалась длинная последовательность разрядов и интервалов (включений и выключений, или байтов) – если быть точнее, десять тысяч байтов. Но каждый раз это была новая последовательность! Очевидно, у последовательностей байтов должна была быть характеристика или свойство, из‐за которого в одном случае зажигалась красная, а в другом – зеленая лампочка. Что бы это могло быть? Ученые решили вскрыть ящик B и посмотреть, что происходит с последовательностью байтов, когда она достигает цели. Внутри ящика B они обнаружили суперкомпьютер – всего лишь обычный цифровой, серийный суперкомпьютер с обширной памятью, содержащий большую программу и большую базу данных, записанные, разумеется, другими последовательностями байтов. А когда ученые пронаблюдали результаты воздействия входящих последовательностей байтов на эту компьютерную программу, то не обнаружили ничего необычного: входящая последовательность всегда самым заурядным образом попадала в центральный процессор, где в ответ на нее за несколько секунд совершалось несколько миллиардов операций, что всегда завершалось одним из двух исходящих сигналов: 1 (зажигавшим красную лампочку) или 0 (который включал лампочку зеленую). Ученые обнаружили, что в любом случае могут без каких бы то ни было проблем или противоречий объяснить каждый этап причинно-следственной связи на микроскопическом уровне. Они не подозревали воздействия каких-либо мистических сил и, например, когда они делали так, чтобы в суперкомпьютер снова и снова вводилась одна и та же последовательность десяти тысяч байтов, программа в ящике B всегда выдавала один и тот же результат – загоралась красная или зеленая лампочка. Но все это было несколько загадочно, поскольку, хотя исход всегда был одним и тем же, он не всегда достигался при помощи одинаковых промежуточных шагов. На самом деле система почти всегда проходила через разные состояния, прежде чем выдать один и тот же результат. Само по себе это загадкой не было, поскольку программа сохраняла копию каждой введенной в нее последовательности сигналов, а потому, когда в нее во второй, третий или тысячный раз вводилась та же последовательность, состояние памяти компьютера каждый раз немного отличалось. Но результат всегда был одинаков; если в первый раз при вводе конкретной последовательности загоралась красная лампочка, то именно она вспыхивала и при каждом следующем вводе той же последовательности, и та же закономерность была верна для «зеленых» последовательностей (как ученые начали их называть). Соблазнительно было предположить, что все последовательности являются либо «красными» (приводящими к вспышке красной лампочки), либо «зелеными» (приводящими к вспышке зеленой лампочки). Но, конечно же, ученые не проверяли все возможные последовательности – только те, которые передавал ящик A. А потому они решили проверить свою гипотезу, временно нарушив связь между ящиками A и B и вводя вариации последовательностей, передаваемых ящиком A, в ящик B. К их замешательству и изумлению, оказалось, что практически каждый раз, когда они изменяли последовательность, передаваемую ящиком A, загоралась янтарно-желтая лампочка! Можно было подумать, что ящик B распознал, что они вмешались. Однако не было сомнений, что ящик B с легкостью принимал составленные людьми версии «красных» последовательностей, зажигая красную лампочку, и составленные людьми версии «зеленых» последовательностей, зажигая лампочку зеленую. Лишь когда менялся один – или больше, чем один – байт в «красной» или «зеленой» последовательности, обычно – почти всегда – загоралась янтарно-желтая лампочка. «Вы убили его!» – однажды ляпнул кто-то, увидев, как «поддельная» красная последовательность превратилась в янтарно-желтую, и это привело к шквалу рассуждений о том, что красные и зеленые последовательности были в некотором смысле живыми особями – возможно, мужского и женского пола, – тогда как янтарно-желтые – мертвыми. Но как бы привлекательна ни была эта гипотеза, она, как оказалось, никуда не вела, хотя дальнейшие эксперименты с несколькими миллиардами случайных разновидностей последовательностей в десять тысяч байтов длиной и в самом деле позволили ученым уверенно предположить, что в действительности существуют три вида последовательностей: красные, зеленые и янтарно-желтые, – причем янтарно-желтых последовательностей на много, много порядков больше, чем красных и зеленых. Практически все последовательности были янтарно-желтыми. Это сделало открытую учеными закономерность лишь более интригующей и загадочной.
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно