Лучшее в нас. Почему насилия в мире стало меньше - читать онлайн книгу. Автор: Стивен Пинкер cтр.№ 91

Второе, что нужно знать о степенных распределениях: они выглядят одинаково для огромного круга величин. Чтобы понять, почему это так удивительно, давайте сравним степенное распределение с более привычным распределением, которое называют нормальным (также распределением Гаусса или колоколообразным). При измерениях роста мужчин или скорости машин на автомагистрали большая часть данных группируется вокруг среднего значения, уменьшаясь в обоих направлениях и образуя кривую, которая напоминает колокол ^[542]. На рис. 5–9 представлены результаты измерений роста американских мужчин. Как видно, мужчин ростом 177 см достаточно много; тех, чей рост 168 см и 189 см — меньше; совсем мало тех, чей рост 153 или 204 см, и вообще нет таких, кто был бы ниже 57 см или выше 272 см (два экстремума, зафиксированные Книгой рекордов Гиннесса). Отношение крайних значений равно 4,8 — небольшая цифра, и можно поклясться, что вы никогда не встретите человека 5 м ростом.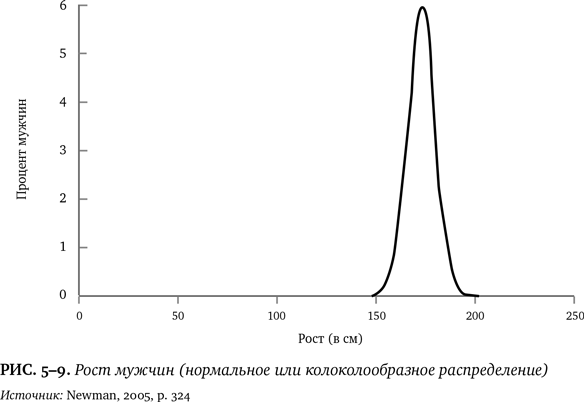

Но есть величины, чьи измерения не группируются у типичного значения, не снижаются симметрично в обоих направлениях и не вписываются в ограниченный диапазон. Размер городов и населенных пунктов — хороший пример. Трудно ответить на вопрос, какого размера типичный американский населенный пункт. В Нью-Йорке живет 8 млн человек; самый маленький американский город, согласно Книге рекордов Гиннесса, — это Даффилд в Виргинии, там живут всего 52 человека. Отношение числа жителей самого большого города к самому маленькому составляет 150 000, что значительно превышает менее чем пятикратный перепад в росте мужчин.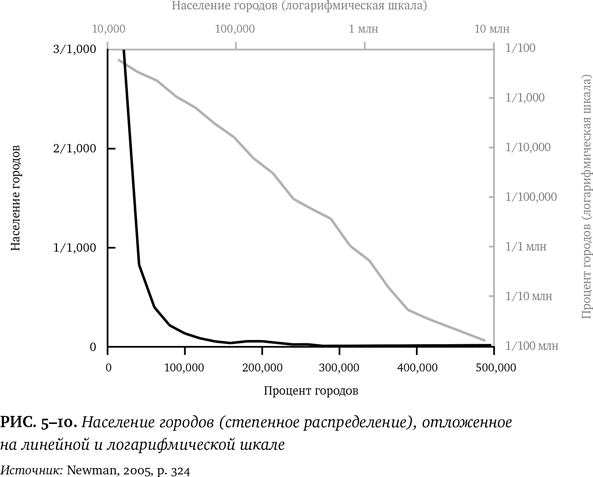

Кроме того, график распределения размеров городов не напоминает по форме колокол. Как показывает черная линия на рис. 5–10, он больше похоже на букву L с высокой спинкой слева и длинным хвостом справа. Число городского населения здесь отложено на обычной линейной шкале на горизонтальной оси черного цвета: города с населением 100 000, 200 000 и так далее. Процент городов с соответствующим числом жителей указан на черной вертикальной оси. В трех тысячных процента (3/1000, или 0,003) американских городов число жителей равно 20 000, в двух тысячных процента (2/1000) городов проживает по 30 000 человек, в 1/1000 — по 40 000 человек, и так далее — чем больше население, тем меньше городов ^[543]. Теперь посмотрим на серые оси на графике вверху и справа. На них отложены те же самые числа, но на логарифмической шкале, на которой равномерно распределены не величины сами по себе, а их порядок (количество нолей). Точки, отмечающие размер популяции, — это 10 000, 100 000, 1 000 000 и так далее. Процент городов с определенным количеством жителей тоже ранжируется согласно порядку величины: 0,01 %, 0,001 %, 0,0001 % и так далее. Когда координатные прямые выстроены таким образом, с распределением происходит нечто любопытное: L вытягивается в ровную линию. Значит, перед нами степенное распределение.

И это возвращает нас к теме войны. Так как войны подчиняются законам степенного распределения, некоторые из его математических свойств помогут нам понять природу войн и порождающие их механизмы. Начать с того, что степенные распределения с экспонентой, как в случае с войнами, даже не имеют среднего значения. Нет такой вещи, как типичная война, и нельзя ожидать, что, достигнув определенного числа жертв, война естественным образом сойдет на нет.

Кроме того, степенные распределения не масштабируемы. Спускаетесь вы или поднимаетесь по логарифмическому графику, они всегда выглядят одинаково — как прямая линия. С точки зрения математики это значит, что, какие бы единицы вы ни рассматривали — большие или малые, распределение выглядит неизменным. Предположим, что компьютерные файлы в 2 Кб составляют четверть от файлов в 1 Кб. Если же сделать шаг назад и посмотреть на файлы более высокого ранга, мы обнаружим то же самое: файлы в 2 Мб составляют четверть от файлов в 1 Мб, а файлы в 2 Тб составляют четверть от файлов в 1 Тб. Что касается войн, можно размышлять так: каковы шансы, что маленькая война, скажем в 1000 смертей, перейдет в войну средних размеров — в 10 000 смертей? Шансы таковы же, как в случае, когда средняя война в 10 000 смертей превратится в большую войну в 100 000 смертей, или большая война в 100 000 смертей в масштабную войну в 1 000 000 смертей, или масштабная война в мировую.

И третье свойство степенных распределений — наличие так называемого толстого хвоста, когда предельные значения существуют в количествах, которыми нельзя пренебречь. Вы никогда не встретите пятиметрового человека и не увидите машину, летящую по автостраде со скоростью 500 км в час. Но вы вполне можете найти город с 14 млн жителей, или книгу, продержавшуюся в списке бестселлеров 10 лет, или лунный кратер, такой огромный, что он виден с Земли невооруженным глазом, — или войну, которая стала причиной гибели 55 млн человек.

Толстый хвост степенного распределения, который с подъемом по шкале магнитуд опускается полого, а не отвесно, означает, что предельные значения крайне маловероятны, но не абсолютно невероятны. Это важная разница. Шансы встретить пятиметрового человека равны нулю, это абсолютно невероятно, и вы можете головой поклясться, что этого никогда не случиться. Но шансы, что город вырастет до 20 млн жителей или что книга будет бестселлером 20 лет подряд, всего-навсего крайне маловероятны: скорее всего, этого не случится, однако можно вполне предположить, что когда-нибудь это произойдет. Что это значит применительно к войнам, понятно без объяснений. Крайне маловероятно, что мир столкнется с войной, в которой погибнет 100 млн человек, и еще менее вероятно, что какая-нибудь война приведет к гибели миллиарда живущих. Но в век ядерного оружия наше охваченное ужасом воображение и математика степенного распределения сходятся в одном: это не абсолютно невероятно.

До сих пор мы рассматривали причины войн как платоновские абстракции, как будто армии выходят на поле боя прямиком из уравнений. Что нам на самом деле нужно понять, так это почему войны распределяются по степенному закону, какая комбинация психологии, технологии и политики генерирует этот паттерн. Сегодня у нас нет убедительного ответа. Степенное распределение могут порождать самые разные механизмы, и доступные нам сведения о войнах не настолько точны, чтобы определить, какие из них действуют здесь.

Однако немасштабируемая природа распределения кровопролитных конфликтов может дать нам представление о движущих силах войны ^[544]. Первое, что приходит в голову: размер не имеет значения. Во всех случаях действует одна и та же психологическая динамика — динамика теории игр, которая решает, будут ли стороны конфликта угрожать, пасовать, блефовать, открывать огонь, обострять ситуацию, продолжать сражаться или отступать, причем не важно, являются ли противоборствующие коалиции уличными бандами, отрядами боевиков или армиями великих держав. Скорее всего, так случается, потому что люди — социальные животные, вступающие в союзы, которые объединяются в коалиции и так далее. И на каждом уровне организации эти коалиции могут столкнуться по воле какой-нибудь политической группировки или одного человека — главаря банды, босса мафии, полевого командира, короля или императора.