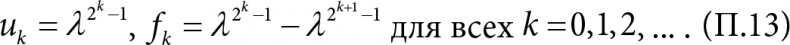
Это так называемый двойной экспоненциальный закон. Двойка в формуле, та самая двойка – вторая степень – из выражения (П.10). Точно так же мы могли бы выбирать не из двух, а из r серверов и получили бы
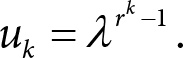
Интересно заметить, что при тех же предположениях, но случайном выборе одного сервера, изменятся выражения (П.10) и, соответственно, (П.11). Действительно, на этот раз заявка выбирает только один сервер и вероятность попасть на сервер с k или больше заявками равна просто иk. Тогда вместо (П.12) получаем классическое уравнение баланса:
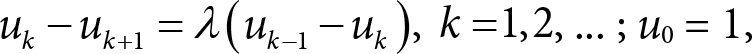
решение которого задается известной формулой Эрланга:
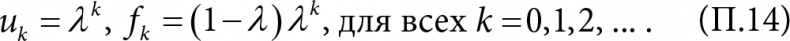
Очевидно, что иk в формуле (П.13) убывает гораздо быстрее.
Именно эти формулы мы использовали в
табл. 5.1
. В нашем случае λ = 0,9, и в таблице мы привели значения fk. В первой колонке – значения k, во второй – значения fk, подсчитанные по формуле (П.14), в третьей – значения fk, подсчитанные по формуле (П.13).
Назад к Главе 5
Приложения к главе 6
1. Схема Диффи – Хеллмана
Для начала введем обозначения. Пусть р – заданное простое число, g – заданное натуральное число, g < p. На самом деле g это так называемый первообразный корень числа р. Об этом мы расскажем ниже, в
приложении 2
и
приложении 3
к главе 6. Цель данного раздела – доказать, что в схеме Диффи – Хеллмана Алиса и Боб действительно получают один и тот же ключ.
Для любых натуральных чисел n и р мы воспользуемся стандартным обозначением для остатка от деления n на р:
n(mod p) = [остаток от деления n на p].
(Читается «n по модулю p».)
Итак, Алиса задумала число х, а Боб число у. Схема Диффи – Хеллмана состоит из двух шагов.
Шаг 1. Алиса передает Бобу
a = (gx) (mod p).
Боб передает Алисе
b = (gy) (mod p).
Шаг 2. Алиса вычисляет ключ
KA = (bx) (mod p).
Боб вычисляет ключ
KB = (ay) (mod p).
Утверждение. Боб и Алиса получили один и тот же ключ K = KA = KB.
Доказательство. Нам нужно доказать, что KA = KB. Поскольку а и b – это остатки от деления на р, то существуют такие целые числа k и l, при которых
a = gx − kp, b = gy − lp.
Подставив эти выражения в формулы для ключей, получаем:
KA = (gy − lp)x (mod p),
KB = (gx − kp)y (mod p).
Заметим, что в выражении для KA можно расписать (gy − lp)x следующим образом:
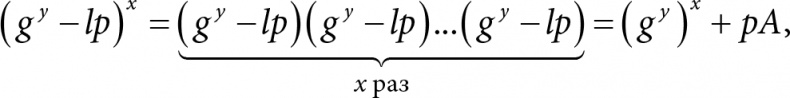
где А – это целое число, то есть рА делится на р. Таким образом получаем
KA = ((gy − lp)x) (mod p) = ((gy)x + pA) (mod p) = (gy)x (mod p).
Совершенно аналогично для какого-то целого числа B получаем
KB = ((gx − kp)y) (mod p) = ((gx)y + pB) (mod p) = (gx)y (mod p).
Результат теперь очевиден, поскольку
(gy)x = gyx = gxy = (gx)y.
2. Дискретное логарифмирование
Вспомним, что логарифм числа у по основанию g – это такое число х, для которого выполняется
gx = y.
Легко заметить, что очень похожая операция лежит в основе схемы Диффи – Хеллмана.
После возведения в степень мы берем остаток от деления на р. Как мы уже упоминали выше, в математике такая операция обозначается gx (mod p) (читается «g в степени х по модулю р»). При этом, естественно, g и х натуральные числа и у g нет общих делителей с р.


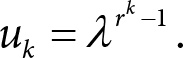
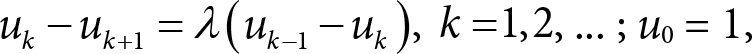
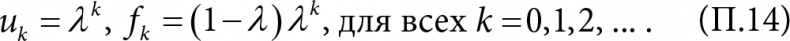
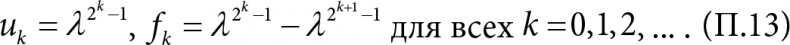
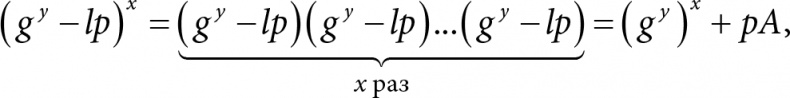
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно