
|
||
|
|
||
|
|
Онлайн книга - Кому нужна математика? Понятная книга о том, как устроен цифровой мир | Автор книги - Нелли Литвак , Андрей Райгородский
Cтраница 34

Число сочетаний вычисляется по формуле 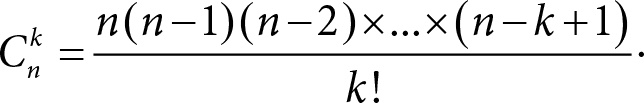
Мы приводим вывод этой известной формулы ниже, в приложении 3. Легко проверить, скажем, что C¹n, и действительно мы можем выбрать одну позицию из n ровно n способами. Значит, всего внутри шара 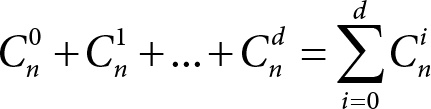
слов. Здесь слагаемое C0n=1 – это число слов, отстоящих от центра на расстояние 0. Такое слово только одно – сам центр. Поскольку шары с центрами в кодовых словах попарно не пересекаются, то всего в них находится 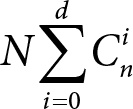
различных слов. Но это количество заведомо не превосходит числа всех возможных кодовых слов, которое, как мы уже знаем, равно 2n. Таким образом, 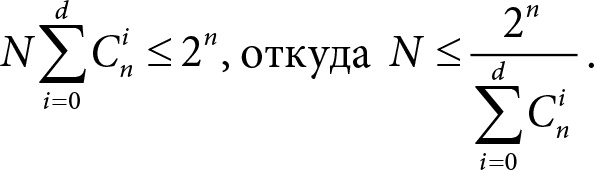
Эта формула и есть граница Хэмминга. В нашем примере, когда n = 10, d = 2, получаем 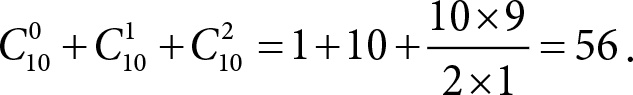
Всего последовательностей длины 10 ровно 210 = 1024. Получается, что максимальное количество кодовых слов не превышает 1024 ÷ 56 ≈ 18,2857. Поскольку число кодовых слов целое, оно не больше 18. 3. Число сочетаний из n по k
Мы рассмотрим число сочетаний на примере, связанном с кодированием. Давайте попробуем сосчитать, сколько существует слов длины n и веса k, k ≤ n. Напомним, что слово – это запись из нулей и единиц, а его вес – это количество единиц. Значит, нам нужно выбрать из n позиций k штук для расстановки на этих k выбранных позициях единиц. При этом ясно, что как только позиции будут выбраны, кодовое слово определяется однозначно. Выбрали, скажем, из шести позиций первую, четвертую и пятую – все, появилось кодовое слово 100110. Хорошо, допустим, есть n позиций. Выбираем из них любую. Это можно сделать n способами. Для каждого из этих n способов выбора первой позиции из оставшихся n − 1 позиций снова выбираем любую. Для этого уже есть только n − 1 вариант. Итого количество способов зафиксировать первую и вторую позиции для единиц равно n (n − 1). Точно так же три позиции можно последовательно выбрать одним из n (n − 1) (n − 2) способов. И так далее. Для данного k будет всего n (n − 1) (n − 2) × … × (n − k + 1) вариантов. Это и есть ответ? Не совсем! Заметим, что в нашем примере, где n = 6 и k = 3, мы могли сначала выбрать, например, первую позицию, затем – четвертую и наконец – пятую, а могли сперва выбрать четвертую позицию, затем – пятую и лишь в конце – первую. И для каждого из подобных вариантов у нас получится одно и то же кодовое слово 100110. Сколько же раз в нашей формуле n (n − 1) (n − 2) × … × (n − k + 1) мы тем самым посчитали одно и то же кодовое слово? Смотрите, получая эту формулу, мы выбирали какие-то последовательности номеров позиций: допустим, это были 1-4-5, 1-5-4, 5-1-4, 5-4-1, 4-1-5, 4-5-1. Видно, что все эти последовательности дают одно и то же слово из нулей и единиц. И видно, что их 6. Чтобы снова прийти к этому выводу не путем унылого перебора (которым мы сейчас занимались), а «весело и с умом», надо рассудить так: из трех чисел 1, 4, 5 мы можем сначала выбрать любое (3 варианта); затем вслед за ним расположить второе уже только одним из двух способов, а третье выбирается однозначно. Рассуждение дает нужный результат: число способов упорядочить числа 1, 4, 5 равно 3 × 2 × 1 = 6. Аналогично для любого k возникает формула k (k − 1) × … × 2 × 1 = k!. Напомним: по принятой в математике конвенции 0! = 1. Что же мы имеем в итоге? Сначала мы вывели формулу n (n − 1) (n − 2) × … × (n − k + 1), потом сообразили, что в ней каждое множество позиций для единиц учтено k! раз. Это означает, что искомое количество кодовых слов равно 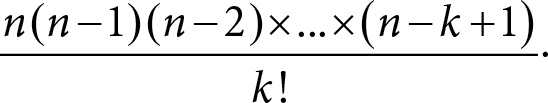
Заметим, что найденное выражение можно переписать в виде 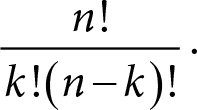
Это так называемое число сочетаний из n по k, или биномиальный коэффициент. В настоящее время для него приняты два обозначения: 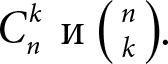
Назад к Главе 3 Приложения к главе 4
В качестве дополнительного материала к этой главе рекомендуем книгу Андрея «Модели случайных графов» {33} . Там в подробностях приводится доказательство теоремы Эрдеша – Реньи и много других интересных результатов из теории случайных графов. 1. Вероятность потери связи в мини-сети |
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно