
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 23

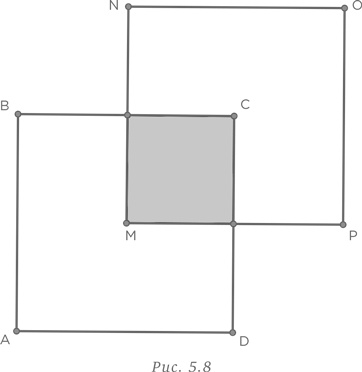
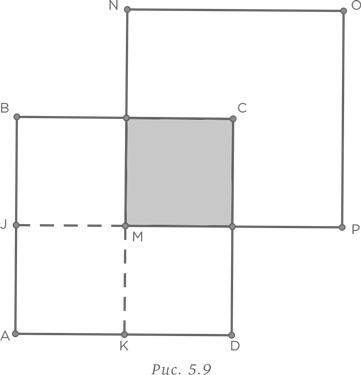
Если этого недостаточно, чтобы удостовериться в равенстве закрашенной области четверти исходного квадрата, то нужно лишь продолжить линии PM и NM до пересечения со сторонами квадрата в точках J и K соответственно, как показано на рис. 5.9. Очевидно, что закрашенная область равна
Задача 5.10
Найдите значение x, которое удовлетворяет уравнению:
Обычный подход
На первый взгляд задача кажется настолько ошеломляющей, что большинство людей не знают, как к ней подойти. И это не удивительно. Образцовое решение
Посмотрим на это, как на своего рода экстремальную ситуацию. Начнем с того, что количество x в этом ряду бесконечно. Отбрасывание одной неизвестной x не должно никак влиять на результат в силу характера бесконечности. Таким образом, удалив первую неизвестную x, мы обнаружим, что все оставшиеся x так же должны быть равны 2. Это позволяет переписать уравнение, как x2 = 2. Следовательно x = ±√2. Если ограничиться положительными числами, то ответом будет x = √2. Ниже показано, как с увеличением ряда значение приближается к 2. 
Вот мы и нашли удивительно простое решение для очень сложной на первой взгляд задачи. Задача 5.11
В одной из старейших телевизионных игр под названием Let's Make a Deal участникам предлагают сделать слепой выбор. Случайно выбранный зритель выходит на сцену и видит перед собой три двери, за одной из которых находится автомобиль, а за двумя другими — ослы. Участник надеется выбрать ту дверь, за которой спрятан автомобиль, а не ту, где стоит осел. Если он угадывает, то получает автомобиль в качестве приза. Однако не все так просто. После того, как участник сделает выбор, ведущий, Монти Холл, который знает, за какой дверью находится автомобиль, показывает одного из ослов (не открывая две оставшиеся двери) и спрашивает участника, хочет ли он оставить первоначальный выбор (что кроется за ним пока неизвестно) или, может быть, передумает и выберет другую неоткрытую дверь. В этот момент, чтобы повысить напряжение, публика начинает скандировать «оставить» или «передумать». Вопрос в том, что делать? Есть ли разница? Если так, то какую стратегию лучше использовать (т. е. что может повысить вероятность выигрыша)? Обычный подход
Кто-то скажет, что лучше всего принимать решение интуитивно. Большинство, однако, придерживаются мнения, что в любом случае разницы никакой нет, поскольку у вас один шанс из двух получить автомобиль. И те и другие неправы, а раз так, то есть серьезный мотив, разобраться что к чему. Образцовое решение
Лучше всего рассмотреть эту задачу шаг за шагом, а потом, для уверенности, рассмотреть экстремальную ситуацию и принять решение. 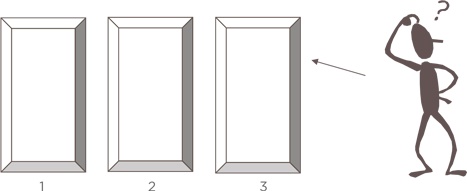
Разберем задачу шаг за шагом. Результат постепенно станет ясным. За дверями находятся два осла и один автомобиль. Вы должны попытаться получить автомобиль. Вы выбираете дверь 3. Монти Холл открывает одну из дверей, которую вы не выбрали, и показывает осла. 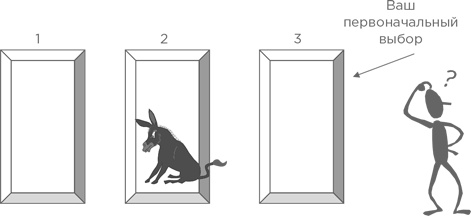
Он спрашивает: «Вы все еще хотите оставить свой первоначальный выбор или передумаете и выберете другую закрытую дверь?» Чтобы помочь принять решение, воспользуемся стратегией анализа экстремальных ситуаций. Допустим, у нас 1000 дверей, а не три. 
Вы выбираете дверь 1000. Какова вероятность того, что это правильная дверь? «Очень маловероятно», поскольку вероятность выбора правильной двери равна
Насколько вероятно, что автомобиль находится за одной из других дверей (1–999)? «Очень вероятно»:

|
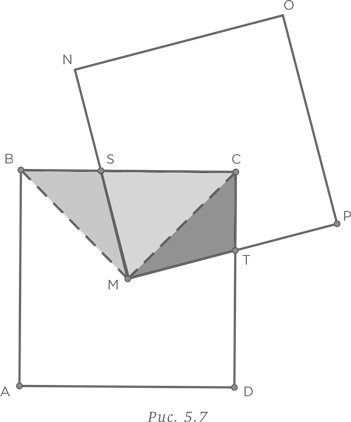
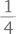 площади квадрата, или
площади квадрата, или
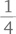 части 16 см2, т. е. 4 см2. Разместив квадраты в определенном положении, мы легко нашли ответ.
части 16 см2, т. е. 4 см2. Разместив квадраты в определенном положении, мы легко нашли ответ.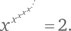
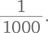
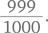
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно