
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 20

Обычный подход
Обычно 450 последовательно делят на нечетные числа (1, 3, 5, …) до тех пор, пока не найдут частное в виде простого числа. Это в конечном итоге дает результат, но может потребовать довольно много времени. Образцовое решение
Воспользуемся нашей стратегией и посмотрим на задачу с другой точки зрения. Число 450 можно записать как 2 × 32 × 52. Поскольку 32 и 52 это нечетные числа, а 450 — четное число, то единственным возможным четным простым множителем для 450 является 2. Таким образом, нечетное число равно 32 × 52 = 225. Задача 4.18
Число 1 000 000 имеет множество пар целочисленных множителей, т. е. двух чисел, произведение которых равно 1 000 000. Однако существует только одна пара множителей, которые не содержат нулей. Чему равны эти множители? Обычный подход
Традиционный подход — это перебор пар чисел, произведение которых равно 1 000 000, в поисках пары, не содержащей нулей. Можно начать с 1 × 1 000 000, 2 × 500 000 и т. д. Это наверняка потребует много времени — ведь у числа 1 000 000 масса пар множителей. Образцовое решение
Проанализируем число 1 000 000 с другой точки зрения. Это число можно представить как 106. Степень, в свою очередь, можно разложить следующим образом: (2 × 5)6 = 26 × 56. Это дает нам два множителя, которые не содержат нулей: 26 = 64 и 56 = 15 625. Обратите внимание на то, что все остальные пары множителей должны содержать как минимум один ноль, поскольку при перемножении чисел 2 и 5 получается 10, а это дает число, оканчивающееся на ноль. Глава 5
Анализ экстремальных ситуаций Иногда, чтобы решить задачу, полезно присвоить одним переменным экстремальные значения, а другие переменные сохранить постоянными. Если на переменные не налагаются какие-либо ограничения, то экстремальный сценарий может дать полезные результаты. Большинство из нас подсознательно использует эту стратегию в реальной жизни. Мы, например, спрашиваем себя: «Что может произойти в самом плохом случае?» Определение «наихудшего сценария» — это образчик использования стратегии поиска экстремальной ситуации, которая иногда помогает очень изящно решить проблему. Допустим, вас просят протестировать новый продукт, скажем, хозяйственное мыло. Вам необходимо испытать его в очень холодной и в очень горячей воде, т. е. рассмотреть две экстремальные ситуации, чтобы получить значимый результат. Если оно хорошо работает при экстремальных температурах, то должно вести себя так же и при промежуточных температурах. Бывает, что использование экстремумов для решения задачи противоречит здравому смыслу. Например, когда возникает вопрос, что лучше, бежать под дождем, чтобы добраться из точки А в точку В, или двигаться медленно, мы вспоминаем, что при быстрой езде на автомобиле под дождем ветровое стекло заливает водой, а при более медленном движении потоки воды не такие сильные. Так что лучше, бежать во время дождя или нет? Анализ экстремальных ситуаций показывает, что очень медленное движение увеличивает время, которое мы находимся под дождем, а экстремально медленное движение, скажем, с нулевой скоростью, приведет к тому, что вы промокнете до нитки. Таким образом, чем быстрее мы будем двигаться, тем меньше намокнем. Вот так экстремумы помогают решать задачи. Рассмотрим задачу, где стратегия анализа экстремумов помогает найти решение. В 40 почтовых ящиков в местном почтовом отделении каждое утро кладут письма. Однажды почтальон разложил по этим ящикам 121 письмо. Закончив работу, он обнаружил, что в одном ящике больше писем, чем в любом другом. Какое наименьшее количество писем может находиться в этом ящике? Поскольку в задаче требуется найти наименьшее количество писем в ящике, мы можем рассмотреть следующую экстремальную ситуацию. Распределим письма равномерно. Предположим, что во всех ящиках находится одинаковое количество писем. Это экстремальная ситуация, противоположностью которой является ситуация, когда все письма лежат в одном ящике. При равномерном распределении в каждый ящик попадает 3 письма — 120: 40 = 3. Добавление дополнительного письма в один из ящиков доведет количество писем в нем до 4 — это и будет наибольшее число. Таким образом, наименьшее количество писем в почтовом ящике, которое превышает количество писем в любом другом ящике, равно 4. Чтобы попрактиковаться в применении этого метода, рассмотрим еще одну задачу, на этот раз со статистическим уклоном: Кларисса написала 5 целых чисел. Как оказалось, их мода равна 12, а медианное значение — 14. Среднее арифметическое (или просто среднее) этих чисел равно 16. Одно из чисел больше медианного значения на 5. Какие именно числа написала Кларисса? Воспользуемся стратегией анализа экстремальной ситуации. Поскольку мода равна 12, наихудший сценарий (наименьшее значение) — это два раза по 12. Мы знаем также, что медиана, или среднее значение равно 14. Так как одно число больше медианы на 5, оно составляет 14 + 5, или 19. Итак, нам известны следующие числа: 12, 12, 14, 19. Среднее находится путем сложения всех пяти чисел и деления суммы на 5. Поскольку среднее равно 16, то сумма всех чисел составляет 16 × 5 = 80. Найдем сумму уже известных чисел 12 + 12 + 14 + 19 = 57. Недостающее число должно быть равным 80–57 = 23. Таким образом, Кларисса написала следующие числа: 12, 12, 14, 19, 23. Обратите внимание, насколько важно было начать решение с анализа экстремальной ситуации, который позволил определить, что числовой ряд включает в себя два числа 12. При применении данной стратегии следует, однако, соблюдать осторожность. Анализируя экстремальную ситуацию, следите за тем, чтобы не изменить переменную, которая влияет на другие переменные, а также не изменить сам характер задачи. Задачи, представленные в этой главе, помогают понять, в каких ситуациях можно использовать рассматриваемую стратегию. Задача 5.1
Автомобиль едет по шоссе с постоянной скоростью 55 км/ч. Водитель замечает другой автомобиль на расстоянии
Обычный подход
Традиционное решение заключается в составлении таблицы «скорость × время = расстояние», как рекомендуют многие учебные пособия. Это делается следующим образом: |
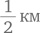 позади. Второй автомобиль обгоняет первый 1 минуту спустя. С какой скоростью двигался второй автомобиль, если считать, что она была постоянной?
позади. Второй автомобиль обгоняет первый 1 минуту спустя. С какой скоростью двигался второй автомобиль, если считать, что она была постоянной? Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно