
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 18

Второе выражение можно упростить, разбив числа на простые множители следующим образом: 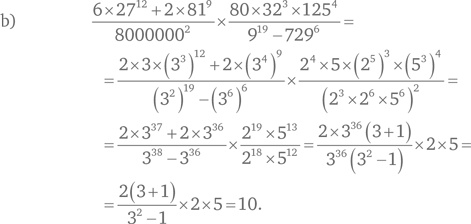
Задача 4.10
И у Вольфганга, и у Людвига есть целое число евро, причем каждое из них меньше 100. Когда они посчитали свои деньги, оказалось, что три четверти суммы Вольфганга равны двум третям суммы Людвига. Какое максимальное число евро может быть у каждого из них? Обычный подход
Первая реакция — применить алгебраический подход. Мы можем составить одно уравнение с двумя неизвестными. Пусть W представляет количество евро у Вольфганга, а L — количество евро у Людвига. Наше уравнение имеет следующий вид: 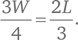
Умножим обе части уравнения на 12 и получим: 9W = 8L. Решение уравнения для W дает следующий результат: 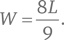
Поскольку у каждого из мальчиков по целому числу евро, сумма Людвига должна быть кратной 9, т. е. 9, 18, 27, 36, …, 99. Теперь можно подставить каждое из этих чисел в уравнение и определить количество евро у Людвига. Наибольшее количество евро, которое может иметь Людвиг, составляет 11 × 9, или 99 евро (менее, чем 100). Мы знаем, что
Образцовое решение
Воспользуемся арифметическим подходом и взглянем на задачу с другой точки зрения. Поскольку
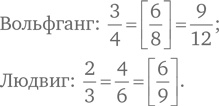
Если у Вольфганга 8 евро, а у Людвига 9 евро, то части их сумм становятся одинаковыми и равными 6 евро. Поэтому ответ должен быть равен произведению одного и того же множителя на 8 и 9. Таким образом, наибольшая сумма, которую может иметь Людвиг, составляет 11 × 9, или 99 евро, а наибольшая сумма Вольфганга — 11 × 8, или 88 евро. Ответ можно проверить, определив величину
Задача 4.11
На рис. 4.3 ширина прямоугольника AEFK равна AK = 8, а длина AE разделена на четыре части AB = 1, BC = 6, CD = 4 и DE = 2. Чему равна площадь четырех закрашенных треугольников? 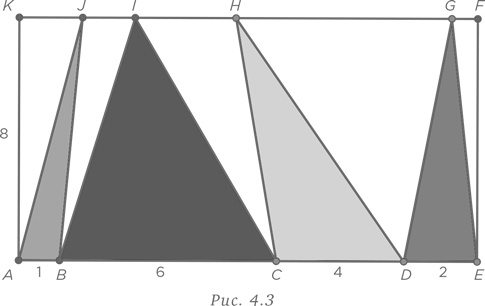
Обычный подход
Очевидный подход — найти площадь каждого из четырех треугольников и сложить их. Во всех четырех случаях высота треугольника равна ширине прямоугольника AK = 8. Таким образом, площади четырех треугольников составляет: 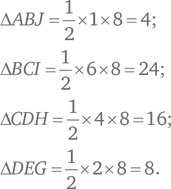
Сумма этих площадей равна 4 + 24 + 16 + 8 = 52. Образцовое решение
Воспользуемся нашей стратегией принятия другой точки зрения на решение задачи. Треугольники имеют одну и ту же высоту, а именно 8. Сумма оснований четырех треугольников равна длине прямоугольника, т. е. 13. Таким образом, площадь четырех закрашенных треугольников равна половине площади прямоугольника, или
Задача 4.12
Определите, сколько чисел можно составить из цифр от 1 до 9 при условии, что цифры в этих числах должны располагаться в порядке возрастания. Обычный подход
Большинство людей, скорее всего, воспользуются методом проб и ошибок и попытаются выяснить, нет ли здесь какой закономерности, и будут добавлять в список одно число за другим, т. е. сначала однозначные числа, затем двухзначные, трехзначные и т. д. Если выполнить эту работу тщательно, то можно получить правильный ответ, однако такой подход трудоемок. |
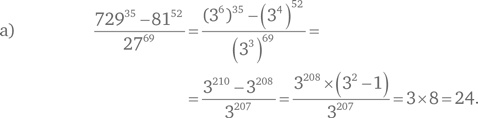
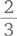 суммы Людвига (66 евро) равны
суммы Людвига (66 евро) равны
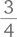 суммы Вольфганга. Таким образом, сумма Вольфганга составляет
суммы Вольфганга. Таким образом, сумма Вольфганга составляет
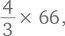 или 88 евро, а сумма Людвига — 99 евро.
или 88 евро, а сумма Людвига — 99 евро.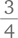 суммы Вольфганга равны
суммы Вольфганга равны
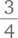 суммы Людвига, найдем эквивалентные дроби с одинаковым числителем:
суммы Людвига, найдем эквивалентные дроби с одинаковым числителем: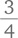 от 88 евро (66) и
от 88 евро (66) и
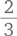 от 99 евро (66).
от 99 евро (66).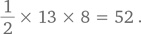
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно