
|
||
|
|
||
|
|
Онлайн книга - Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса | Автор книги - Марио Ливио
Cтраница 43

Теперь предположим, что мы хотим предсказать, какова вероятность, что у случайно выбранного человека из этой популяции IQ окажется между 85 и 100. Рис. 37 подсказывает нам, что эта вероятность – 0,341 (или 34,1 %), поскольку по законам теории вероятности вероятность – это количество желаемых результатов, деленное на общее количество возможностей. А если нам интересно выяснить, какова вероятность, что кто-то (случайно выбранный) из этой популяции обладает IQ выше 130, то взгляд на рис. 37 покажет, что эта вероятность равна примерно 0,022, то есть 2,2 %. Примерно так же, опираясь на свойства нормального распределения и на метод интегрального исчисления (для вычисления площади под кривой), можно вычислить вероятность, что значение IQ попадет в тот или иной заданный диапазон. Иными словами, ответы нам дают теория вероятности и ее половинка-помощница статистика – в сочетании. Как я уже не раз подчеркивал, вероятность и статистика обретают смысл, если имеешь дело с большим количеством событий, но не с отдельными событиями. Этой фундаментальной оговоркой, известной как закон больших чисел, мы обязаны Якобу Бернулли, который сформулировал ее в виде теоремы в своей книге «Ars Conjectandi» («Искусство предположений»; на рис. 38 приведен титульный лист) [95]. В переводе на обыденный язык теорема гласит, что если вероятность, что событие случится, равна p, то p – это самое вероятное соотношение количества случаев, когда это событие происходит, к общему числу попыток. Если же общее число попыток приближается к бесконечности, то доля успешных попыток становится в точности равна p. Вот как Бернулли формулирует закон больших чисел в «Искусстве предположений»: «Еще предстоит выяснить, увеличиваем ли мы при увеличении числа наблюдений и вероятность, что регистрируемое соотношение желаемых случаев к нежелательным приблизится к подлинному значению, и тогда эта вероятность в конце концов превзойдет всякую желаемую точность». Затем он пояснил это на конкретном примере [96]. 
Рис. 36 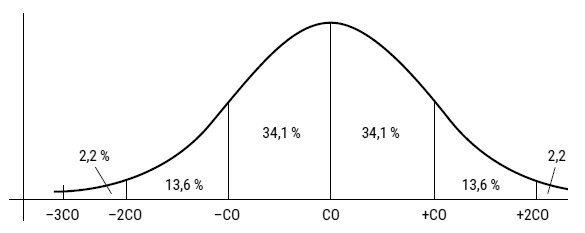
Рис. 37 У нас есть урна с 3000 белых и 2000 черных камешков, и мы хотим эмпирически определить соотношение количества белых и черных камешков – а мы его не знаем, – доставая из урны по одному камешку и записывая, когда нам попадается белый камешек, а когда черный (напоминаю, что при этом процессе должно соблюдаться важное требование: каждый камешек, отметив его цвет, следует положить обратно в урну и лишь затем доставать следующий, чтобы количество камешков оставалось постоянным). А теперь мы спрашиваем, возможно ли, увеличив число попыток, добиться, чтобы стало в 10, 100, 1000 раз вероятнее (а в конечном итоге прийти к «совершенной уверенности»), что соотношение количества извлечений белого камешка к количеству извлечений черного камешка приобретет точно такое же значение (3:2), что и подлинное соотношение черных и белых камешков в урне, а не какое-то другое значение? Если ответ отрицательный, то я признаю, что наша попытка оценить посредством наблюдения соотношение результатов в каждом конкретном случае (например, соотношение количества белых и черных камешков) обречена на провал. Но если это так, то мы наконец-то можем при помощи этого метода приблизиться к совершенной уверенности [в следующей главе «Искусства предположений» Якоб Бернулли доказывает, что так и есть] … и мы можем определять количество случаев a posteriori почти с той же огромной точностью, как если бы оно было известно нам a priori. 
Рис. 38 Оттачиванию этой теоремы Бернулли посвятил двадцать лет, и она стала с тех пор одним из столпов статистики. В заключение он отметил, что убежден в существовании законов, которые управляют всем, – даже в тех областях, которые на первый взгляд представляются случайными. Если бы удалось непрерывно пронаблюдать все события с этой минуты и на протяжении вечности (посредством чего вероятность превратилась бы в конечном итоге в уверенность), оказалось бы, что все в мире, даже то, что кажется нам совершенно случайным, происходит по определенным причинам и в определенном соответствии с законом, и что мы, следовательно, вынуждены предположить наличие определенной необходимости – если угодно, предопределения. Насколько я знаю, именно это имел в виду Платон, когда выдвигал доктрину вселенской цикличности и утверждал, что по истечении бесчисленных веков все вернется к первоначальному состоянию. Мораль этой истории о науке неопределенности очень проста: можно применить математику даже к относительно «ненаучным» областям нашей жизни, в том числе и к тем, которые, как нам кажется, управляются чистой случайностью. Поэтому при попытках объяснить «непостижимую эффективность» математики мы не можем ограничиваться в дискуссии одними лишь законами физики. Рано или поздно нам все равно придется разбираться, что делает математику столь вездесущей. Невероятное могущество математики не ускользнуло и от знаменитого драматурга и эссеиста Джорджа Бернарда Шоу (1856–1950). Несмотря на то, что прославился он отнюдь не математическими достижениями, Шоу написал очень глубокую статью о статистике и теории вероятности под названием «Напасть игры и благодать страховки» («The Vice of Gambling and the Virtue of Insurance») [97]. В этой статье Шоу признает, что в его глазах страховка «основана на фактах, которые невозможно объяснить, и на рисках, которые способны вычислить лишь профессиональные математики». Однако далее он делает следующее проницательное замечание. А теперь представьте себе деловую беседу между купцом, который жаждет торговать за границей, но отчаянно боится потерпеть кораблекрушение или быть сожранным дикарями, и шкипером, который жаждет заполучить грузы и пассажиров. Капитан уверяет купца, что его товары в полнейшей безопасности, как и он сам, буде он пожелает их сопровождать. Однако купец, голова у которого забита приключениями Ионы, Св. Павла, Одиссея и Робинзона Крузо, на это не отваживается. Разговор у них пойдет примерно так.
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно