Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса - читать онлайн книгу. Автор: Марио Ливио cтр.№ 46

Позвольте мне сделать здесь небольшую паузу, чтобы уяснить значение выражения «произвольно выбрать». В течение тысячелетий евклидова геометрия считалась уникальной и неизбежной – единственно верным описанием пространства. А когда стало ясно, что можно выбирать постулаты произвольно и получать при этом не менее логичное описание пространства, вся концепция перевернулась с ног на голову. Надежная, тщательно выстроенная дедуктивная схема вдруг стала больше похожа на игру, в которой постулаты играли роль правил и не более того. Возьмешь другие постулаты – сыграешь в другую игру. Это открытие имело поистине сокрушительные последствия для понимания природы математики.

Почву для решительной атаки на евклидову геометрию подготовили сразу несколько математиков, обладавших широким мировоззрением. Особенно выделялись среди них иезуит Джироламо Саккери (1667–1733), исследовавший то, к каким последствиям может привести замена пятого постулата каким-то другим утверждением, и немецкие математики Георг Клюгель (1739–1812) и Иоганн Генрих Ламберт (1728–1777), которые первыми поняли, что могут существовать и другие геометрии, альтернативные евклидовой. И все же нужен был кто-то, кто забил бы последний гвоздь в крышку гроба представлений о том, что единственное возможное описание пространства – это евклидова геометрия. Заслуга принадлежит троим математикам – из России, Венгрии и Германии.

Первым, кто опубликовал целый трактат о новом типе геометрии – геометрии, выстроенной на поверхности в форме выгнутого седла (рис. 41, а) – был русский математик Николай Иванович Лобачевский (1792–1856; рис. 42). В геометрии такого рода (получившей название гиперболической геометрии) пятый постулат Евклида заменен утверждением, что если даны линия на плоскости и точка, лежащая на этой плоскости вне данной прямой, через эту точку параллельно данной прямой можно провести не менее двух прямых. Другое важное отличие геометрии Лобачевского от Евклидовой заключалось в том, что если у Евклида сумма углов треугольника всегда равна 180° (рис. 41, b), то у Лобачевского она всегда меньше 180°. Поскольку работа Лобачевского была напечатана в никому не известном журнале «Казанский вестник», она прошла практически незамеченной, пока в конце 1830 годов не стали появляться переводы на французский и немецкий. Молодой венгерский математик Янош Бойяи (1802–1860), ничего не знавший о работе Лобачевского, разработал похожую геометрию в 1820-е годы ^[103]. Полный юношеского энтузиазма, Янош писал в 1823 году своему отцу Фаркашу Бойяи (рис. 43): «Я открыл такое великолепие, что сам потрясен… я из ничего создал совершенно новый мир». К 1825 году Янош уже был готов показать старшему Бойяи первые черновики новой геометрии. Рукопись называлась «Наука о пространстве, абсолютно истинная» ^[104]. Несмотря на восторг молодого человека, его отец сильно сомневался в том, что в идеях Яноша есть здравое зерно. Тем не менее он решил опубликовать новую геометрию в виде приложения к собственному двухтомному трактату об основах геометрии, алгебры и анализа (которому дал завлекательное, по своему мнению, название «Рассуждение о началах математики для прилежной молодежи»). Экземпляр книги Фаркаш послал в июне 1831 года своему другу Карлу Фридриху Гауссу (1777–1855; рис. 44) – не просто самому выдающемуся математику того времени, но человеку, которого наряду с Архимедом и Ньютоном считают одним из трех величайших математиков всех времен. Однако из-за свирепствовавшей тогда холеры книга затерялась, и Фаркаш был вынужден послать второй экземпляр. Шестого марта 1832 года Гаусс написал ему ответ, и высказанные там замечания не оправдали надежд юного Яноша.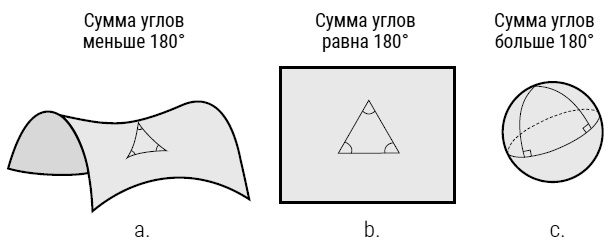

Рис. 41

Рис. 42

Рис. 43

Рис. 44

Позвольте подчеркнуть, что Гаусс, очевидно, боялся, что последователи Канта, которых он называл «беотийцами» (для древних греков это было синонимом дураков), сочтут это философской ересью. Гаусс продолжал.

Фаркаш был вполне удовлетворен похвалой Гаусса – он считал, что она «очень приятна», – зато Янош совершенно опустил руки. Почти десять лет он отказывался верить, что Гаусс по праву претендует на первенство, и его отношения с отцом, который, как он считал, поспешил рассказывать Гауссу о его результатах, сильно осложнились. Когда же Янош наконец обнаружил, что Гаусс и в самом деле начал работать над этой задачей еще в 1799 году, то очень озлобился – и все его последующие труды по математике, а он оставил по себе около двадцати тысяч рукописных страниц, по сравнению с юношескими достижениями были весьма посредственны.