Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса - читать онлайн книгу. Автор: Марио Ливио cтр.№ 42

1. Наследование той или иной черты предполагает передачу неких «факторов» (сегодня мы зовем их генами) от родителей потомству.

2. Каждый потомок наследует от каждого родителя по одному такому «фактору» (для каждой отдельной черты).

3. Отдельная черта может не проявиться у потомка, однако передаться следующему поколению.

Но как же объяснить количественные результаты опытов Менделя? Мендель утверждал, что у каждого растения-родителя должно быть два идентичных «фактора» (сегодня мы назвали бы их аллелями – вариантами гена), либо два желтых, либо два зеленых (как на рис. 35). При скрещивании каждый потомок наследует две разные аллели, по одной от каждого родителя (согласно вышеприведенному правилу 2). То есть каждое зерно потомка содержит желтую аллель и зеленую аллель. Почему же тогда в этом поколении все зерна желтые? Мендель объяснил, что желтый – доминирующий цвет и он маскирует присутствие в этом поколении зеленой аллели (правило 3). Однако (опять же в соответствии с правилом 3) доминантный желтый не мешает рецессивному зеленому передаваться следующему поколению. В следующем туре скрещивания каждое растение, содержащее одну желтую и одну зеленую аллель, опыляется другим растением, содержащим ту же комбинацию аллелей. Поскольку потомство содержит по одной аллели от каждого родителя, зерна следующего поколения могут содержать следующие комбинации (рис. 35): зеленая – зеленая, зеленая – желтая, желтая – зеленая или желтая – желтая. Все зерна с желтой аллелью становятся желтыми, потому что желтый цвет – доминантный.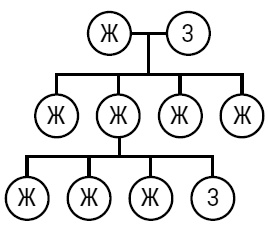

Рис. 34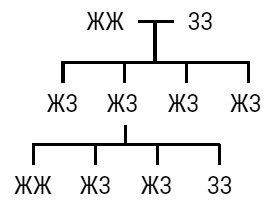

Рис. 35

Следовательно, поскольку у всех комбинаций равные шансы на возникновение, отношение желтых зерен к зеленым должно составлять 3:1.

Вы, возможно, заметили, что весь эксперимент Менделя, в сущности, ничем не отличается от эксперимента по бросанию двух монет. Назовем зеленые аллели орлами, а желтые – решками и зададимся вопросом, какая доля зерен будет желтой (с учетом того, что доминантная желтая аллель определяет цвет зерен), – и это будет то же самое, что спрашивать о вероятности получить по крайней мере одну решку при бросании двух монет. Очевидно, вероятность равна ¾, поскольку решка есть в трех из возможных четырех результатов (решка – решка, решка – орел, орел – решка, орел – орел). Это значит, что соотношение количества бросков, где получается по крайней мере одна решка, к количеству бросков, где нет ни одной решки, в конечном итоге приблизится к 3:1, как в экспериментах Менделя.

Хотя Мендель опубликовал статью «Опыты по гибридизации растений» в 1865 году (и выступил с докладами на двух научных конференциях), его открытия остались незамеченными – и были обнаружены лишь в начале ХХ века ^[93]. Точность полученных результатов вызывала некоторые сомнения, но, тем не менее, Менделя считают основоположником математического подхода к современной генетике (см., например, Fisher 1936). Авторитетный английский статистик Рональд Эйлмер Фишер (1890–1962) по следам Менделя заложил фундамент популяционной генетики, отрасли математики, которая занимается распределением генов в популяции и расчетами изменения частотности генов со времени ^[94]. Сегодня генетики опираются на статистические выборки в сочетании с исследованиями ДНК для прогнозирования возможных характеристик еще не рожденного потомства.

Но все же – как связаны статистика и вероятность?

Стремясь разобраться в эволюции Вселенной, ученые обычно подходят к этой проблеме с обеих сторон. Одни начинают с тончайших колебаний ткани мироздания в первичной Вселенной, другие изучают все подробности нынешнего состояния Вселенной. Первые разрабатывают масштабные компьютерные модели, которые показывают, как Вселенная развивалась с течением времени. Вторые занимаются детективной работой – пытаются дедуктивно вычислить прошлое Вселенной по множеству характеристик ее нынешнего состояния. Примерно таковы и отношения между теорией вероятности и статистикой. В теории вероятности заданы переменные и первоначальное состояние, и ее цель – предсказать наиболее вероятный конечный результат. В статистике известен результат, но не определены причины, которые к нему привели.

Рассмотрим простой пример того, как эти две области встречаются, так сказать, посередине и дополняют друг друга. Начнем с того факта, что статистические исследования показывают, что измерения самых разных физических величин и даже человеческих черт распределяются согласно кривой нормального распределения. Но на самом деле кривая нормального распределения – это не какая-то одна кривая, а целое семейство кривых, описываемых одной и той же общей функцией, и все они полностью характеризуются всего двумя математическими величинами. Первая из них – среднее значение – это центральное значение, относительно которого распределение симметрично. Эта величина зависит, разумеется, от того, какую именно переменную измеряют (рост, вес, IQ и так далее). Среднее значение одной и той же переменной может быть разным в разных популяциях. Например, средний рост шведов, скорее всего, отличается от среднего роста перуанцев. Вторая величина, определяющая кривую нормального распределения, называется стандартным отклонением. Это мера того, насколько тесно данные сосредоточены вокруг среднего значения. На рис. 36 у кривой нормального распределения (а) самое большое стандартное отклонение, поскольку значения рассеяны шире. Однако тут мы сталкиваемся с интересным фактом. Если с помощью интегрирования сосчитать площадь под кривой, легко математически доказать, что независимо от среднего значения и величины стандартного отклонения, 68,2 % измерений лежат в области, ограниченной одним стандартным отклонением по обе стороны от среднего значения (рис. 37). Иначе говоря, если среднее значение IQ в определенной (крупной) популяции равно 100, а стандартное отклонение равно 15, то 68,2 % людей в этой популяции обладают IQ между 85 и 115. Более того, для всех кривых нормального распределения 95,4 % всех случаев лежат в пределах двух стандартных отклонений от среднего, а 99,7 % данных попадают в пределы трех стандартных отклонений по обе стороны от среднего (рис. 37). Из этого следует, что в вышеприведенном примере 95,4 % популяции обладают IQ между 70 и 130, а 99,7 % – между 55 и 145.