
|
||
|
|
||
|
|
Онлайн книга - Игра случая. Математика и мифология совпадения | Автор книги - Джозеф Мазур
Cтраница 20

Слабый закон больших чисел, примененный к любому событию, вероятность которого равна p, говорит нам, что вероятность
Итак, что же здесь происходит? Похоже, что у более высокого N есть некоторая свобода от закона больших чисел, поскольку в масштабах больших чисел больше места для незаметных ошибок. Для 5000 бросков были 2561 орел и 2439 решек с разностью 122. Это дает ошибку в 2,4 %, что не так уж плохо. Но, если не знать распределение этих орлов, может случиться так, что 122 орла были выброшены последовательно. Придерживаясь этой точки зрения, представьте, что 758 решек выброшены последовательно за 67 500 бросков или 694 орла выброшены последовательно за 82 500 бросков. Другими словами, нет математического закона, который исключает возможность последовательного выпадения огромного числа орлов при большом N. 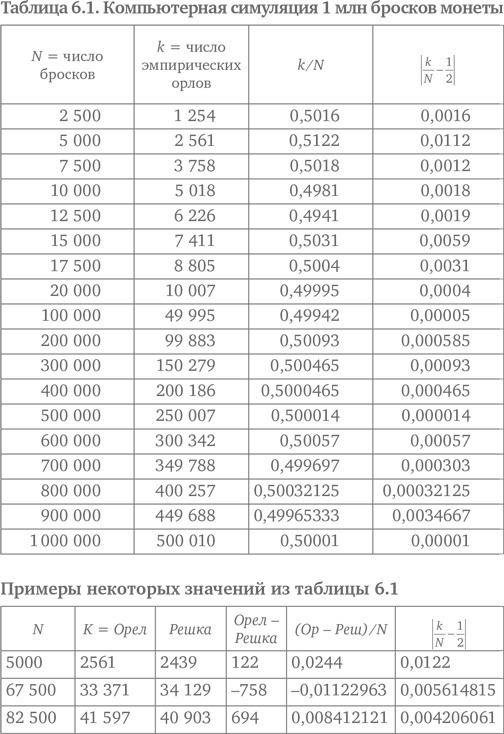
Глава 7
Треугольник Паскаля В физическом мире не существует совершенной симметрии, искусственных машин с бесконечно малым допуском или идеальных моделей. Это мир множества скрытых переменных, явления которого слишком трудно охватить точной мерой. Иными словами, подлинные случайности действительно происходят, и мы часто обращаемся к вероятностным картинам событий, чтобы понять сложный феномен случайности. Что если бы у вас обнаружили миелодиспластический синдром – редкую форму рака, при котором костный мозг не вырабатывает достаточно красных кровяных телец? Вы столкнулись бы с дилеммой: согласиться на трансплантацию костного мозга с 70 % вероятностью успеха или не делать ничего и с 70 % вероятностью умереть в течение следующих 10 лет. Конечно, у трансплантации имеются свои риски. Помимо необходимости химиотерапии и риска инфекции будет еще 30 % вероятность смерти в течение следующих 6 месяцев. Брайан Зикмунд-Фишер, который преподает теорию рисков и теорию вероятностей в Медицинской школе Мичиганского университета, столкнулся с такой дилеммой в 1998 г. Ему диагностировали миелодиспластический синдром и сказали, что без лечения он проживет всего 10 лет, а с лечением у него будет 70 %-ная вероятность жить нормальной жизнью {63}. Он сделал ставку на трансплантацию. Смысл в том, что шансы ничего не говорят об отдельном человеке. Вероятность в 70 % получена посредством сбора статистических данных о сотнях (возможно, тысячах) людей, которые столкнулись с той же дилеммой, – государственная, нелокальная статистика. Статистические группировки описывают тенденции и возможности, а не отдельные случаи, когда можно выиграть или проиграть. Возьмем некое событие, которое вы могли бы счесть редким. Его математические шансы могут быть один к миллиону, но, вероятно, такие цифры связаны с тем, что событие оценивается как локальный феномен. В качестве примера можно взять белку, которую ударило молнией в тот момент, когда она пересекала дорогу. Когда мы говорим на этом знакомом языке шансов, то часто выражаемся фигурально, без какого-либо последовательного метода определения терминов. Итак, «один на миллион» обычно применяется к событию, которое, как мы думаем, происходит в довольно широких пределах Соединенных Штатов. Но США – большая страна. Это нетрудно увидеть, пролетев над маленькими домиками, маленькими деревьями и обширными зелеными полями. Мы не думаем ни о том, сколько там внизу белок, ни о том, сколько из них пересекают дорогу в отдельный момент времени. Ученые оценивают численность белок в США в 1,12 млрд, что в 3 раза больше населения страны. И белки постоянно пересекают дороги. Учитывая 1,12 млрд белок, 6,5 млн км дорог и 9,5 млн км2 площади США, вполне возможно, что каждую минуту 300 белок пересекают дороги {64}. Во время грозы это число может быть даже больше. В среднем в Соединенных Штатах случается 110 000 гроз в год. Летом гроз гораздо больше, чем зимой, что делает возможность поражения белки ударом молнии летом действительно очень большой. Каждое явление в природе вызывается большим числом неопределенных возможностей. Когда бросают игральную кость, то результат сильно зависит от ее начального положения в руке бросающего и значительно слабее – от звуковых волн, создаваемых голосами присутствующих в комнате. Это лишь два внешних фактора, направляющих кость к положению, в котором она остановится. То, как она ударяется об стол, точность ее балансировки, ее движение по руке, упругость соударения со столом – все это повлияет на то, какая из сторон будет направлена вверх, когда кость остановится. Рассмотрим игру, в которой возможен только выигрыш или проигрыш, а вничью сыграть невозможно. Пусть X обозначает исход испытания, а P (X) – вероятность наступления этого исхода. Если бы вы, например, бросали монету, P (орел) равнялось бы 1/2, как и P (решка). В колесе для американской рулетки 38 ячеек, включая 0 и 00: 18 красных; 18 черных; 0 и 00 – зеленые. Если вы ставите на красное, P (красное) равняется 18/38 или, если упростить, 9/19, а P (не красное) равняется 10/19. Если бы вы бросали игральную кость, надеясь выбросить «очко» (1), то P (1) равняется 1/6. Выберите любую подобную игру и спросите себя: какова вероятность выиграть 0, 1, 2, 3 или 4 раза? Вполне уместный вопрос, поскольку реальные азартные игры предполагают совокупные последовательности выигрышей или проигрышей. Вспомним о Джоан Гинтер, о том, как она 4 раза выиграла в лотерею. Вам также могут быть интересны шансы сыграть лучше, чем если бы вы остались при своих, или по крайней мере шансы не проиграть больше 2 из 4 ставок.
|
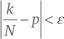 приближается к 1 по мере увеличения N. Возьмем ԑ = 0,0001 (выбрано произвольно) с p = 1/2 для ситуации с бросанием монеты и спросим, насколько возможно, что
приближается к 1 по мере увеличения N. Возьмем ԑ = 0,0001 (выбрано произвольно) с p = 1/2 для ситуации с бросанием монеты и спросим, насколько возможно, что
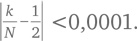 Обратите внимание (табл. 6.1), что
Обратите внимание (табл. 6.1), что
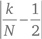 имеет резкие перепады при низких значениях N. Но они, очевидно, есть также и при высоких значениях. От 100 000 до 200 000 оно увеличивается. Даже с 800 000 до 900 000 оно увеличивается, пока не падает на миллионе. Создается обманчивое впечатление, что разность между орлом и решкой приближается к нулю. Но ничего не говорится о волатильности этого приближения при увеличении числа испытаний. Как мы видим, волатильность увеличивается по мере увеличения числа бросков монеты.
имеет резкие перепады при низких значениях N. Но они, очевидно, есть также и при высоких значениях. От 100 000 до 200 000 оно увеличивается. Даже с 800 000 до 900 000 оно увеличивается, пока не падает на миллионе. Создается обманчивое впечатление, что разность между орлом и решкой приближается к нулю. Но ничего не говорится о волатильности этого приближения при увеличении числа испытаний. Как мы видим, волатильность увеличивается по мере увеличения числа бросков монеты. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно