Игра случая. Математика и мифология совпадения - читать онлайн книгу. Автор: Джозеф Мазур cтр.№ 23

Итак, каждая кривая биномиального распределения трансформируется с помощью математического трюка (посредством сдвигов и масштабирования) в особую могущественную кривую нормального распределения, график которой изображен на рис. 7.4 ^{75}.

Числа в основании кривой на рис. 7.4 – это стандартные отклонения от среднего. Мы объединили испытания в группы по стандартному отклонению. Отдельные вероятности исходов событий теперь не видны. Переменная X под кривой на рис. 7.4 показывает отклонение числа эмпирических успешных исходов от наиболее вероятного их числа. Иными словами, X, переменная горизонтальной оси, измеряется в стандартных отклонениях. Высота кривой – это уже не вероятность, поскольку мы ее масштабировали и сжали, сохранив площадь под кривой. Но в обмен на это масштабирование и сжатие мы получаем некоторые ценные сведения. Первое: около 68 % площади под кривой лежат на одном стандартном отклонении от среднего и около 95 % площади – на двух стандартных отклонениях от среднего. Второе: одно стандартное отклонение отмечено точками перегиба, т. е. точками на кривой, где кривая меняет форму с вогнутой на выпуклую.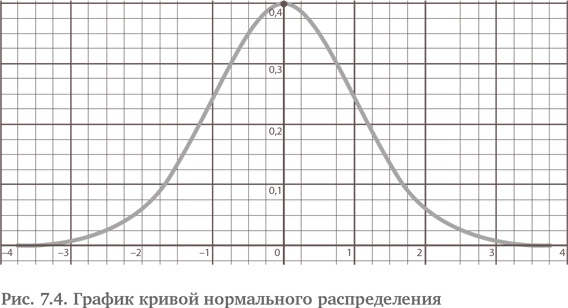

Хотя одно стандартное отклонение для исхода «красное» в 100 турах рулетки – это не то же самое, что стандартное отклонение для орла в 100 бросках монеты, чудесным образом кривая и в том и в другом случае одинакова. Но толкование значения этих кривых будет различным. Хотя кривая на рис. 7.4 может быть одинаковой для распределения в различных азартных играх, разметку на осях нужно рассматривать в соответствии с конкретными расчетами среднего и стандартного отклонения. Эти данные будут зависеть от числа туров и вероятностей положительных исходов для конкретных игр.

Когда мы исследуем частотное распределение, то склонны смотреть в основном на отклонение от наиболее вероятного значения. Но то, что происходит далеко за пределами наиболее вероятных значений, может иметь невероятно сильное воздействие на общий накопленный результат. Мы обращаем мало внимания на эту внешнюю область, потому что в основном думаем о центре распределения и явлениях, которые наиболее вероятны, а не о том, что могло бы произойти в самых маловероятных случаях.

Принимаем ли мы в расчет маловероятные ситуации самых плохих сценариев? Или говорим, что они настолько редки, что их следует просто отбросить? Это и есть совпадения или случайности природы, реальные физические явления, движущиеся с попутным ветром вероятности. По мере увеличения числа бросков «правильной» монеты общее число орлов может значительно превысить общее число решек (или наоборот). Например, ситуация, когда вы бросаете монету 100 раз и каждый раз выпадает орел, маловероятна, но возможна, несмотря на то что шансы выбросить орла при каждом подбрасывании 1 к 1. Все же будем немного более сдержанны и рассмотрим случай, где из 100 бросков мы имеем исходы в 41 орел и 59 решек, или вероятности 0,41 и 0,59 соответственно ^[13]. Похоже, что разница велика, но из 100 бросков разница между орлом и решкой на самом деле всего лишь 18. Однако, если вы бросите монету 500 раз (как мы сделали в главе 6) и найдете, что вероятности стали значительно ближе к 1/2, скажем, где пропорция орлов в общем числе бросков равняется 0,45, а решек – 0,55, итого у нас будет 225 орлов и 275 решек, разность составит 50.

Иными словами, разность может продолжать увеличиваться, даже если коэффициенты приближаются к 1/2. Добавим к этому понимание, что для распределения результатов нет прогноза, мы находим его по мере того, как увеличивается число бросков, и то же самое происходит с вероятностью возникновения все большего и большего числа непрерывных серий орлов. Мы могли бросить монету 100 раз, сделать паузу, бросить еще 100 раз, снова сделать паузу и продолжить дальше подобным образом. Каждый раз мы могли бы начинать вести счет заново. Тогда каким же образом выходит, что разность между решками и орлами может быть 50 за 500 бросков, но, возможно, 10 за 100 бросков? Когда случится разница в 50? Может ли она случиться на последних 100 бросках подряд? Конечно, это тоже будет совпадением, но у каждой возможности есть небольшой шанс!

В теории в рулетку играют шариком идеально сферической формы, который крутится и ударяется о безупречно сбалансированное колесо с идеально ровными ячейками в совершенно неподвижной комнате в мире, который мы никогда не видели и который никогда не существовал. Реальные ставки делают в физическом мире, где шарики и колеса производятся с предельно жесткими допусками, но эти шарики и колеса изготавливают машины, созданные человеком. Магическая связь между идеальным и физическим настолько замысловата, что наше непонимание ослепляет нас.

В физическом мире мы могли бы исследовать подлинные колеса для рулетки на предмет их недостатков, составив таблицу наблюдений, которую можно изобразить как график распределения частот. Такой график будет совершенно не похож на график нашей идеальной модели, но если колеса действительно были «правильные» и если бы мы рассмотрели достаточное число туров, то график эмпирических результатов должен быть похож (по крайней мере по форме) на график на рис. 7.4. Если мы выполним n испытаний в эксперименте, у нас будет n эмпирических результатов O₁, O₂, O₃…., Oⁿ с соответствующими вероятностями p₁, p₂, p₃,…, pⁿ, дающими эмпирическое распределение вероятностей. Например, как мы отметили ранее в случае с игрой в кости, исходом может быть выпадение одной из шести сторон, вероятность каждой из которых – 1/6. В честной игре экспериментальная версия распределения должна быть близка к теоретическому распределению, но мы, конечно, признаем, что непременно будут некоторые расхождения, поскольку мир неидеален.

В данном контексте идеальный значит математический. Понимание реальных шансов исходит из сравнения данных, полученных в ходе наблюдений, с расчетами, ожидаемыми в идеальном мире. Игроки могут знать, что шансы не в их пользу, и все же надеяться на то, что физический мир отклонится от математических ожиданий в пользу их ставки. Корни такого поведения кроются к могущественной идее о том, что кто-то должен выиграть. Они будут сильно рисковать, не обращая внимания на математические ожидания фортуны.

Проанализировав опубликованные записи, сделанные в ходе 4 недель в июле и августе 1892 г. в казино в Монте-Карло, английский математик Карл Пирсон обнаружил, что механизм, который был настолько точен и выверен, насколько это вообще возможно для рулеточного стола, все же не вполне следовал законам вероятности ^{76}. Если допустить математическую точность, то шарик с одинаковой вероятностью падает в любую из 37 ячеек колеса.