Игра случая. Математика и мифология совпадения - читать онлайн книгу. Автор: Джозеф Мазур cтр.№ 18

Доказательство Бернулли опирается на число возможных комбинаций предметов, и их расчет не имеет ничего общего со случайными поворотами фортуны. Эдит Дадли Силла, известная переводчица «Искусства предположений», говорит, что Бернулли объяснял связь посредством теологии. Она писала: «Он уверяет, что в сознании или воле Бога есть четкие и определенные ситуации, известные Богу вечно, и со временем проявляющие себя в опыте или наблюдении». Говоря о «вечности», она имеет в виду то, что Бернулли игнорировал фактор времени в расчетах коэффициентов успешности случайных событий. Силла указывает на следующий довод Бернулли: «Нет существенной разницы между тем, чтобы выбросить желаемым образом одну игральную кость в течение некоторого времени, и тем, чтобы бросить сразу такое число игральных костей, которое равнялось бы числу сделанных бросков одной кости» ^{55}.

Ожидание, измеряемое математическим ожиданием (мы дадим определение ниже), – это упряжь, которой взнузданы тайны неопределенности. Вместе со стандартным отклонением, которое измеряет объем того, что выпадает из ожидания, оно дает нам возможность рассмотреть стохастический (случайный) мир. Две эти величины – математическое ожидание и стандартное отклонение – колеса и винтики статистики частотного распределения, показывающей насколько приближаются данные к некоему центральному значению. Чудесным образом с помощью этих величин и простой алгебры у нас есть если не прямое управление, то по крайней мере теоретическое измерение феноменологической вероятности посредством слабого закона больших чисел. В физическом мире каждый бросок игральных костей и каждое падение шарика для пинг-понга определяется большим количеством изменчивых сил и обстоятельств, которые едва ли возможно измерить (скорость, траектория, воздушные потоки, гироскопический эффект, момент инерции, столкновения и т. д.), все же определимые в идеальном мире математики.

В 1657 г. голландский математик и астроном Христиан Гюйгенс опубликовал работу «О расчетах в азартных играх» (De Ratiociniis in Aleae Ludo), которая еще полвека оставалась главным учебником по теории вероятностей ^{56}. Это первая из напечатанных работ, указывающая на отличие между числом успешных исходов и возможным числом успешных исходов ^{57}:

Гюйгенс дает пример азартной игры, где для участия необходимо платить. Человек прячет три монеты в одной руке, семь – в другой; вы выбираете руку и забираете спрятанные в ней монеты. Чтобы продолжать игру, вы должны платить. Но вот в чем вопрос: сколько вам следует платить за игру? Первое утверждение Гюйгенса дает нам ответ: «Если я могу ожидать либо события a, либо b и любое может выпасть мне с одинаковой легкостью, то можно сказать, что мое ожидание будет равняться (a + b)/2». Ответ – 5, иначе говоря, ожидаемая выгода (сумма, которую вы ожидаете получить взамен), или среднее 3 и 7. Совсем не очевидно, что Гюйгенс понимал, какую поразительную силу будет иметь эта идея для будущего анализа рисков, азартных игр и собственно науки. Но он точно понимал, что ядро теории вероятностей – это просто математическое ожидание. Для математика середины XVII в. было бы совершенно преждевременно узнать истину: что все случайные процессы в природе, включая аннуитет, страхование, метеорологию и медицину, а также азартные игры, можно в той или иной мере предсказывать с помощью вычисления математического ожидания. Вообще математическое ожидание можно вычислить, умножив вероятность на размер выплаты. В большинстве случаев это средневзвешенное значение всех возможных величин, которые могут возникать; в качестве весов берутся вероятности. Это сумма всех возможных значений, после того как каждое значение умножено на вероятность его возникновения. В этом есть смысл; в конце концов вы ожидали бы получить 50 центов с доллара, если бы бросали монетку и ставили бы каждый раз по доллару на орла.

Например, возьмем лотерею Texas Lotto. В табл. 5.1 показаны результаты совпадения 3, 4, 5 и 6 чисел. Чтобы получить математическое ожидание от игры, перемножим вероятность и размер выплаты по каждому возможному совпадению и сложим все возможные совпадения.

Если мы предположим, что джекпот равняется, скажем, $2 млн, тогда математическое ожидание составляет 0,000000038 ($2 000 000) + 0,00001115 ($2000) + 0,000654878 ($50) + 0,013157894 ($3) = $0,171517582. Другими словами, реальная стоимость каждого играющего билета – всего 17 центов.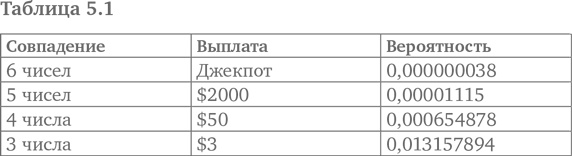

На том раннем этапе истории теории вероятностей люди использовали математическое ожидание как меру риска, не зная, что оно окажется самым естественным показателем центра распределения – склонности данных группироваться вокруг некоего центрального значения, как показано на рис. 5.3.

Согласно данным Всемирной организации здравоохранения, доля рождения мальчиков к общей рождаемости по всему миру составляет 0,515. ^{60} Если рассмотреть данные по конкретным регионам или странам, то шансы далеки от равных. В Мексике доля новорожденных мальчиков очень низкая, тогда как в США и Канаде их доля выше 0,5 ^{61}. Однако для всего населения Земли – а оно уже больше 7 млрд – шансы рождения мальчиков по отношению к девочкам почти равны. Причина проста: у человеческого сперматозоида равное число X и Y хромосом, и у каждой из них равные шансы в момент зачатия. Это бросок правильной монеты.