На плечах гигантов - читать онлайн книгу. Автор: Стивен Хокинг cтр.№ 27

Вторую степень родства, по рождению, следует понимать так: во-первых, некоторые гармонические отношения чисел родственны тому или иному брачному союзу или семейству, а именно – идеальные отношения родственны единственному семейству куба, и наоборот, если отношение невозможно точно выразить в числах и нельзя показать численно любым другим способом, кроме длинной последовательности цифр, которая к нему постепенно приближается, то такое отношение называется божественным, если оно совершенно, и оно различными способами управляет брачным союзом додекаэдра. Подобным же образом это отношение отражают следующие консонансы, или гармонии: 1:2 и 2:3, а также 2:3 и 5:8. Ибо самым несовершенным образом это отношение выражено в 1:2, более совершенно – в 5:8, а еще совершеннее – если мы сложим 5 и 8 и получим 13, а затем сделаем 8 числителем, если это соотношение не перестанет быть гармоническим.

Далее, при построении стороны тела следует разделить диаметр сферы, и тогда октаэдр требует бисекции, куб и тетраэдр – трисекции, а брачный союз додекаэдра – деления на пять. Подобным же образом отношения между фигурами распределяются в соответствии с числами, выражающими эти отношения. Однако квадрат диаметра тоже делится, то есть квадрат стороны тела формируется из определенной доли диаметра. А затем квадраты сторон сравниваются с квадратом диаметра, и соотношения получаются следующие: у куба 1:3, у тетраэдра 2:3, у октаэдра 1:2. По этой причине, если сопоставить два отношения, то кубическое и тетраэдрическое даст 1:2, кубическое и октаэдрическое 2:3, октаэдрическое и тетраэдрическое 3:4. Стороны додекаэдрического брачного союза иррациональны.

В-третьих, гармонические отношения во многом свойственны и уже построенным фигурам. Ведь можно сопоставить количество сторон грани с количеством ребер у тела в целом, и тогда получаются следующие отношения: у куба 4:12, то есть 1:3; у тетраэдра 3:6, то есть 1:2; у октаэдра 3:12, то есть 1:4; у додекаэдра 5:30, то есть 1:6; у икосаэдра 3:30, то есть 1:10. Можно также сопоставить количество сторон грани с количеством граней, и тогда куб даст 4:6, то есть 2:3; тетраэдр 3:4; октаэдр 3:6, то есть 1:2; а додекаэдр с его супругой 5:20 или 3:12, то есть 1:4. Можно также сопоставить количество граней с количеством пространственных углов, и тогда кубический брак даст 6:8, то есть 3:4, у тетраэдра отношение равно единице, у додекаэдрического брачного союза 12:20, или 3:5. А можно сравнить число всех сторон с числом пространственных углов, и у куба это отношение равно 8:12, то есть 2:3, у тетраэдра – 4:6, то есть 2:3, у октаэдра 6:12, то есть 1:2, у додекаэдра 20:30, то есть 2:3, а у икосаэдра 12:30, то есть 2:5.

Далее, можно сравнить друг с другом и сами тела, если тетраэдр поместить, то есть геометрически вписать, в куб, а октаэдр – в тетраэдр внутри куба. Тетраэдр составит треть куба, октаэдр – половину тетраэдра и одну шестую куба, точно так же как октаэдр, вписанный в сферу, составит одну шестую куба, описанного вокруг сферы. Отношения остальных тел иррациональны.

Четвертая же разновидность, или степень, родства сильнее связана с темой этой книги: следует найти отношение сфер, вписанных в тела, к сферам, описанным вокруг них, и рассчитать гармонические отношения, которые приблизительно их описывают. Ведь лишь у тетраэдра диаметр вписанной сферы рационален по отношению к описанной сфере, то есть составляет одну треть ее. Но в кубическом брачном союзе отношение (оно там единственно) рационально лишь в квадрате. Ибо диаметр вписанной сферы относится к диаметру описанной как квадратный корень отношения 1:3. А если составить отношения друг с другом, то отношения тетраэдральных сфер составляет квадрат отношения кубических сфер. В додекаэдрическом брачном союзе отношение опять же единственно, однако иррационально и чуть больше 4:5. Поэтому отношение сфер куба и октаэдра характеризуется следующими консонансами: оно 1:2 (чуть больше) и 3:5 (чуть меньше). А отношение додекаэдрических сфер приблизительно описывается консонансами 4:5 и 5:6 (чуть больше) и 3:4 и 5:8 (чуть меньше).

Но если по некоторым причинам 1:2 и 1:3 приписаны кубу, отношение сфер куба к отношению сфер тетраэдра будет таким же, как отношение консонансов 1:2 и 1:3, которые приписывались кубу, к 1:4 и 1:9, которые следует приписать тетраэдру, если пользоваться этой пропорцией. Ведь эти отношения также представляют собой квадраты этих консонансов. А поскольку 1:9 – не гармонический консонанс, его место в тетраэдре занимает ближайшее отношение 1:8. Однако, согласно этой пропорции, додекаэдрическому брачному союзу соответствуют приблизительно 4:5 и 3:4. Ведь подобно тому, как отношение сфер куба приблизительно равно кубу додекаэдрического отношения, кубические консонансы 1:2 и 2:3 примерно равны кубам консонансов 4:5 и 3:4. Ведь 4:5 в кубе равно 64:125, а 1:2 равно 64:128. Так же и 3:4 в кубе равно 27:64, а 1:3 равно 27:81.

3. Краткое изложение астрономических знаний, необходимых для рассуждений о небесных гармониях

В первую очередь моим читателям следует знать, что древние астрономические гипотезы Птолемея в том виде, в каком они изложены в «Новой теории планет» (Theoricae Novae Planetarum) Пурбаха, а также у других авторов кратких пособий, следует исключить из нашей дискуссии и начисто забыть, ибо они не передают ни истинного положения небесных тел в космосе, ни организации их движения.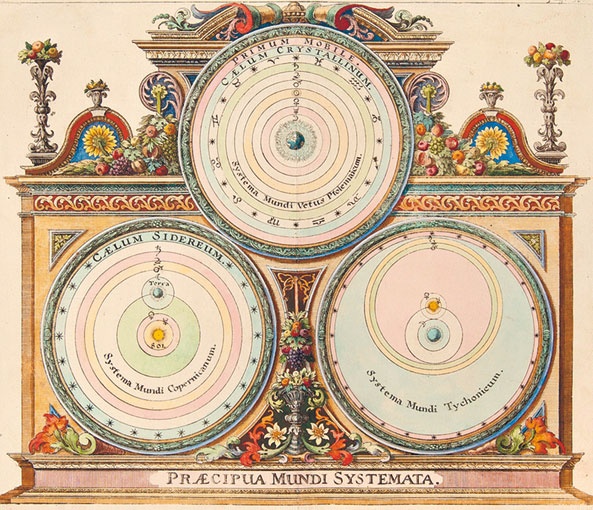

Модели Птолемея, Коперника и Тихо Браге применительно к благо-приятным и неблагоприятным для здоровья периодам, согласным с положением планет. Раскрашенная гравюра из книги «Чудесный мир» (Mundi mirabilis) Иоганна Зана, математика и изобретателя. 1696 год.

Я не могу поступить иначе, кроме как полностью заменить эти гипотезы одной лишь теорией Коперника и по возможности убедить всех в ее истинности, но поскольку для большинства людей образованных она еще в новинку и они по большей части считают нелепицей, что Земля – это одна из планет, которые движутся среди звезд вокруг неподвижного Солнца, те, кого поражает новизна этого мнения, должны знать, что подобные рассуждения о гармониях возможны и на основании теории Тихо Браге, поскольку этот автор придерживается тех же взглядов, что и Коперник, во всем, что касается положения небесных тел и расчета их движения, и лишь переносит годичное продвижение Земли по Копернику на всю систему планетарных сфер и на Солнце, которое, по мнению обоих авторов, находится в центре этой системы. Ведь и при переносе движений остается верным то, что у Браге в любой момент Земля занимает то же место, какое отводит ей Коперник, если не в царстве неподвижных звезд, огромном и неизмеримом, то по крайней мере в системе планетного мира. Как тот, кто чертит круг на бумаге, заставляет вращаться пишущую ножку циркуля, так и тот, кто закрепил бумагу или доску на вращающемся столе, рисует такой же круг неподвижной ножкой циркуля или пером; подобным же образом и в случае Коперника Земля в своем подлинном движении описывает круг посередине между такими же кругами Марса с наружной стороны и Венеры с внутренней; а в случае Тихо Браге вся планетная система (в пределах которой находятся и остальные круги Марса и Венеры) вращается, словно столешница на оси, а неподвижная Земля – это словно бы перо, рисующее круг на этой столешнице между кругами Марса и Венеры; и из такого движения системы следует, что Земля в ее пределах, хотя и остается неподвижной, описывает точно такой же круг вокруг Солнца на полпути между кругами Марса и Венеры, какой у Коперника она описывает при подлинном движении при покоящейся системе. Поэтому, поскольку рассуждения о гармониях касаются эксцентрического движения планет, каким оно видится с Солнца, легко понять, что если наблюдатель находится на Солнце, которое движется как угодно, с его точки зрения Земля, пусть даже она и покоится (если согласиться с Браге), опишет годичный круг на полпути между упомянутыми планетами и за среднее время. Следовательно, если найдется человек столь недалекий, что ему не удастся уловить закономерности движения Земли среди звезд, он все равно получит удовольствие от превосходного спектакля, который поставили самые что ни на есть божественные силы, если он прибавит все, что слышит о ежедневном продвижении Земли по эксцентрике, к рисунку планет относительно Солнца, – к тому самому рисунку, который предлагает Тихо Браге, с неподвижной Землей.