На плечах гигантов - читать онлайн книгу. Автор: Стивен Хокинг cтр.№ 30

Настенная роспись в обсерватории Тихо Браге Ураниборг.

В-девятых [IX], если теперь вы пожелаете той же мерой, так сказать, измерить подлинный путь, который проходит в эфире каждая из этих планет за день, нужно составить два отношения: отношение истинной (невидимой) дневной дуги эксцентрики и отношение средних расстояний каждой из этих планет до Солнца (поскольку это то же самое, что и отношение величины сфер), то есть истинную дневную дугу каждой планеты следует умножить на полудиаметр ее сферы; в результате получатся числа, при помощи которых можно исследовать, состоят ли эти пути в гармонических отношениях.

В-десятых [X], чтобы точно знать, насколько велики будут те или иные дневные пути с точки зрения наблюдателя, расположенного словно бы на Солнце, хотя то же самое можно легко получить из астрономии, но все равно это станет ясно, если умножить отношение путей на обратное отношение не средних, а истинных расстояний, существующих при любом положении на эксцентрике: умножьте путь верхней планеты на расстояние от нижней планеты до Солнца и, наоборот, умножьте путь нижней планеты на расстояние от верхней планеты до Солнца.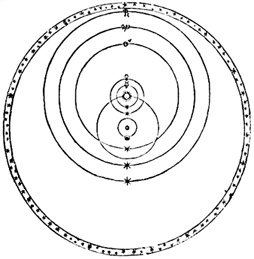

Модель Тихо Браге

В-одиннадцатых [XI], теперь точно так же, если даны видимые продвижения в афелии одной планеты и в перигелии другой – или наоборот либо попеременно, – можно вывести отношения расстояний между афелием одной и перигелием другой. Но где нужно сначала узнать среднее продвижение, то есть обратное отношение периодов, из которого выводится отношение сфер согласно [VIII] выше, тогда, если берется среднее пропорциональное между видимым продвижением любой планеты и ее средним продвижением, это среднее пропорциональное относится к полудиаметру сферы (уже известному) как среднее продвижение к расстоянию, или искомому промежутку. Пусть периоды двух планет – 27 и 8. Поэтому отношение среднего дневного продвижения одной и другой равно 8:27. Поэтому полудиаметры их сфер относятся как 9 к 4. Ведь кубический корень 27 равен 3, а 8 – 2, а квадраты этих корней 3 и 2 равны 9 и 4. Теперь пусть видимое продвижение в афелии одной планеты будет 2, а продвижение другой в перигелии будет 33 и 1/3. Среднее пропорциональное между средними продвижениями 8 и 27 и видимыми будет 4 и 30. Следовательно, если среднее пропорциональное 4 дает среднее расстояние до планеты 9, то среднее продвижение 8 дает расстояние в афелии 18, что соответствует видимому продвижению 2; а если другое среднее пропорциональное 30 дает у другой планеты среднее расстояние 4, то его среднее продвижение 27 даст в перигелии расстояние в 3 и 3/5. Поэтому я утверждаю, что расстояние первой планеты в афелии относится к расстоянию второй планеты в перигелии как 18 к 3 и 3/5. Отсюда очевидно, что если будут найдены консонансы между предельными продвижениями двух планет и для обеих установлены периоды, то из этого однозначно следуют и предельные и средние расстояния, а из них – эксцентрики.

В-двенадцатых [XII], из разных предельных продвижений одной и той же планеты возможно также вывести среднее продвижение. Среднее продвижение – это не в точности арифметическое среднее между предельными продвижениями, не в точности геометрическое среднее, но оно на столько же меньше геометрического целого, на сколько геометрическое целое меньше (арифметического) среднего этих двух средних. Пусть предельные продвижения равны 8 и 10, тогда среднее продвижение будет меньше 9, а также меньше квадратного корня из 80 на половину разности между 9 и квадратным корнем из 80. Таким образом, если продвижение в афелии равно 20, а в перигелии 24, среднее продвижение окажется меньше 22 и даже меньше квадратного корня из 480 на половину разницы между этим корнем и 22. В дальнейшем эта теорема будет применена.

В-тринадцатых [XIII], из всего вышеизложенного можно доказать следующую теорему, которая в дальнейшем будет нам крайне необходима: подобно тому как отношение средних продвижений двух планет обратно пропорционально степени 3/2 сфер, отношение двух видимых сходящихся предельных продвижений всегда меньше отношения степеней 3/2 расстояний, соответствующих этим предельным продвижениям; и в каком отношении произведение двух отношений соответствующих расстояний к двум средним расстояниям или к полудиаметрам двух сфер всегда меньше отношения квадратных корней сфер, в таком же отношении отношение двух предельных сходящихся продвижений превосходит отношение соответствующих промежутков, но если бы это составное отношение превзошло отношение квадратных корней сфер, то отношение сходящихся продвижений оказалось бы меньше, чем отношение их расстояний ^[6].

4. В каких аспектах движений планет Творец выразил гармонические консонансы и как он это сделал

Подобным же образом, если устранить мнимые возвратные продвижения и остановки и отсеять лишь истинные продвижения планет по своим настоящим эксцентрическим орбитам, у планет останутся следующие отличительные свойства: 1) расстояния от Солнца, 2) периоды обращения, 3) дневные эксцентрические дуги, 4) дневные задержки на этих дугах, 5) углы к Солнцу и дневная площадь этих углов, видимая наблюдателю с Солнца. И снова все это, за исключением периодов, меняется в разных участках орбиты, меньше всего в предельных точках, афелии и перигелии, когда планеты отходят от одной предельной точки и движутся к другой, а сильнее всего – на промежуточных участках. Следовательно, когда планета ниже всего и ближе всего к Солнцу и поэтому меньше всего задерживается в одном градусе своей эксцентрики, а, напротив, за один день проходит самую длинную дневную дугу, и с Солнца кажется, что она движется быстрее всего; затем она некоторое время движется одинаково по силе без ощутимых отклонений, пока не минует перигелий, после чего планета постепенно начинает отходить дальше от Солнца по прямой, и в этом самое время дольше задерживается в градусах своего эксцентрического круга, либо, если взять продвижение за один день, то на следующий день планета уходит вперед на меньшее расстояние, и с Солнца кажется, что она движется еще медленнее, пока она не подойдет к высшей апсиде и ее расстояние до Солнца не станет очень большим, ведь тогда она дольше всего задерживается в одном градусе эксцентрики; либо, напротив, за один день она проходит свою самую маленькую дугу, производит гораздо меньше видимого продвижения и проходит наименьшее расстояние по своей общей орбите.

Гармония сфер. Кеплер полагал, что все планеты в нашей Солнечной системе движутся в гармонии, что и отра-жено в этом схематическом изображении Солнечной системы.