Корпорация "Попс" - читать онлайн книгу. Автор: Скарлетт Томас cтр.№ 30

В моноалфавитных используется лишь один шифровочный алфавит. Вот почему их легко разгадать: как только выясняется, какими буквами заменены «е» и «t», понять все прочее становится не сложнее, чем завершить партию игры в «виселицу». В полиалфавитных шифрах, однако, применяются сразу несколько алфавитов. Трудно описать, каким прорывом было предположение Альберти, что можно использовать несколько алфавитов в одной шифровке. Моноалфавитные шифры всегда поддаются разгадке благодаря частотному анализу — даже если не срабатывает метод Шерлока Холмса. Но что, если «исказить» частоты встречаемости букв, сделав так, что одной и той же букве исходника будут соответствовать разные буквы на всем протяжении шифрованного текста? Этот вопрос и задал себе Альберти. И придумал метод, который… ну, гениален, иначе не скажешь. Вы чертите квадрат, состоящий из двадцати шести различных вариантов алфавита — каждый сдвинут на одну букву по отношению к соседним (см. таблицу). Потом выбираете короткое слово-ключ — скажем, RAIN [36] — и пишете его снова и снова поверх текста, который хотите зашифровать, вот так: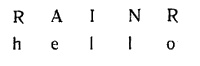

Привет (англ.).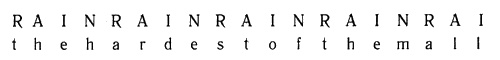

Самый трудный из всех (англ.).

Затем вы с помощью букв слова-ключа определяете, какую строчку «квадрата Вигенера» используете, чтобы зашифровать соответствующую букву сообщения. Буква «h» в слове «hello», зашифрованная по строчке «R», превратится в «Y», «Е», зашифрованная по строчке «А», так и будет «Е» (все, что попадает на строчку «А», остается без изменений, поэтому большинство слов-ключей буквы «А» не содержат). «L», зашифрованная по строчке «I», будет «Т». Однако следующая «l» будет шифроваться по строчке «N» и станет «Y». Таким образом, первое слово — «hello» — превратится в «YETYF», что совсем не похоже на моноалфавитную версию слова. Подсказки в виде сдвоенного диграфа больше нет, а «Y» означает две разные буквы.

Более длинное сообщение, приведенное выше, зашифруется так:

KHMURRLRJTWSKHMZRLT

Вам никогда этого не прочесть при помощи частотного анализа или дедукции. Вам нужно знать, что ключом было слово «RAIN». Это единственный способ справиться с вигенеровым шифром. Конечно, ключ иногда получается просто угадать. После нападения на Всемирный Торговый Центр одна фирма потеряла почти всех своих сотрудников. Немногие уцелевшие решили продолжить дела компании, но оказались перед проблемой: все пароли умерли вместе с теми, кто их знал. Тогда оставшиеся служащие сели и принялись копаться во всех аспектах жизни покойных коллег, записывая названия мест, куда те ездили по выходным, имена домашних животных и так далее, пока не угадали все пароли до единого. Эту историю мне рассказал кто-то на работе — его до глубины души тронул корпоративный дух, проявленный этими людьми. А я просто подумала, что это одна из самых жутких историй, какие я только слышала в жизни.

Хм-м… в общем, учитывая тот факт, что едва ли вы знаете слово-ключ к посланию, смысл которого от вас хотят скрыть, вам нужно пойти путем логики и искать в тексте закономерности — они могут подсказать, какое слово было ключом. Большинство шифровок, конечно, чудовищно сложнее любого учебного примера. Однако мы можем начать искать закономерности в нашем:

KHMURRLRJTWSKHMZRLT

В тексте вроде бы дважды повторен один и тот же триграф, из чего можно сделать два разных вывода. Либо это чисто случайный результат процесса шифровки, и тогда нам от него никакого проку, либо — возможно! — одно и то же слово исходника стояло под одними и теми же буквами ключа и поэтому дважды зашифровалось одинаково; если так, нам это колоссально поможет.

После того как Альберти впервые высказал свои идеи, еще добрых лет триста никто не мог понять, как «взламывать» вигенеровы шифры подобным способом. Это сделал Чарлз Бэббидж, [37] гениально-безумный изобретатель Разностного Двигателя — первой вычислительной машины. Все началось с того, что у него состоялся весьма необычный спор с одним чудаком, который считал, что первым придумал полиалфавитные шифры.

— Я изобрел новый, непробиваемый код!

— Ну, вообще-то он не столь уж нов. О нем известно уже…

— Говорят вам: мой код невозможно взломать!

— Хорошо, пусть так — но вы его не изобретали.

— Вы что, бросаете мне вызов?

— Ладно, если вам так угодно — да, я бросаю вам вызов, дурак вы этакий.

— Тогда посмотрим, как вы с ним справитесь!

Квадрат Вигенера

Так Бэббидж, который не мог не принять вызов, брошенный столь очевидно безголовым человеком, тем более что вызов был полной нелепостью, мимоходом снабдил нас нашим методом. Бэббидж вообще был тот еще тип. Помимо Разностного Двигателя он изобрел также спидометр, скотосбрасыватель (устройство, крепившееся к поездам и счищавшее рогатый скот с путей) и заложил основу современной почтовой системы, позволяющей отправить письмо в любую точку страны за одну и ту же цену. Он понял, что если вы обнаружите закономерности шифра, как в нашем примере — скажем, повторение триграфа «КНМ», — дальше вам стоит действовать следующим образом. Скорее всего, у вас в руках будет шифровка гораздо длиннее; нужно выявить в ней все повторяющиеся буквенные группы. Затем сосчитать количество букв от начала одной группы до начала следующей. В нашем примере вы обнаружите, что от первой «К» до второй — двенадцать букв. Это значит, что количество букв в слове-ключе (которое было написано раз за разом поверх исходника) наверняка является делителем двенадцати, т. е. равно 12, 6, 4, 3, 2 или 1. Такой вывод вполне логичен: если предположить, что те же самые буквы повторяются через двенадцать и в слове-ключе, и в исходнике, то, конечно, это приведет к повтору буквенных групп в шифровке. Двухбуквенный ключ уложится в интервал шесть раз; двенадцатибуквенный — только один. При работе с большим объемом текста обычно удается точно установить делитель, и длина ключа становится очевидной.

Дальше начинаются некоторые сложности. Если вы обнаружили, что ключ состоит из четырех букв, нужно пройтись по всей длине шифровки и обозначить каждую ее букву цифрами 1, 2, 3 и 4, в зависимости от того, какой по счету буквой ключа она была зашифрована. Затем вам нужно произвести частотный анализ каждой выборки; таким образом, для букв, обозначенных единицей, вы получаете вполне определенную частотную таблицу и сравниваете ее со стандартной. Вы повторяете эту операцию для всех остальных выборок и выясняете каждую букву ключа. Дело в шляпе: считайте, вы разгадали послание.