Время переменных. Математический анализ в безумном мире - читать онлайн книгу. Автор: Бен Орлин cтр.№ 40

Движение изменяет форму времени.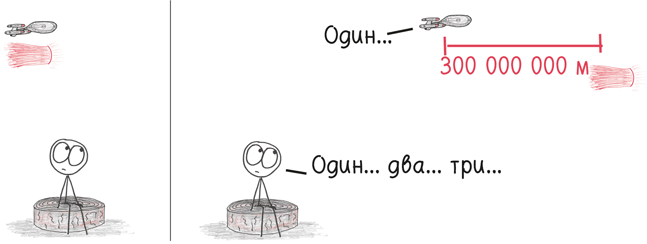

Вам уже кажется, что у вас начались галлюцинации? Тогда вы готовы к следующему шагу: материя изменяет и форму пространства. Солнце, например, не стоит на месте, как мяч для боулинга, лежащий в коробке. Оно, словно мяч для боулинга на надувном матрасе, прыгает по материи, искривляя окружающее пространство-время. Таким образом, когда планета обращается вокруг Солнца или яблоко падает на землю, они не во власти некоего необъяснимого ньютоновского притяжения. Они просто следуют по пути наименьшего сопротивления через изгибающийся четырехмерный ландшафт.

«Материя говорит пространству-времени, как ему изгибаться, – сказал физик Джон Уилер, – а изогнутое пространство говорит материи, как ей двигаться».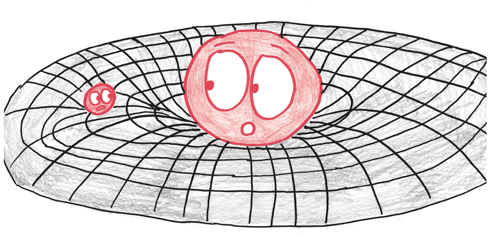

Все это воплотилось в определенную форму в ноябре 1915 г. в уравнении поля Эйнштейна. «Это уравнение умещается на половине строки, – пишет физик Карло Ровелли. – Однако в этом уравнении – целая Вселенная» ^[48]. Оно предсказало, что свет изгибается около тяжелых предметов, что временной поток расширяется по пути из долины к вершине горы, что гравитационные волны могут распространяться через всю Вселенную, что большие звезды могут схлопываться, образуя сингулярности (которые позже получили название «черные дыры»). «Невероятное богатство теории раскрывается в фантасмагорической цепи предсказаний, которые напоминают исступленный бред безумца, – говорит Ровелли, – но все до единого подтвердились» ^[49].

Тем не менее, хотя новые предсказания вылетали из этого уравнения, как патронусы из волшебной палочки, Эйнштейн остался недовольным. Конечно, общая теория относительности могла описать орбитальное движение планет и изгибы потоков фотонов. Но все это были ограниченные, конечные системы. Всего лишь частицы космоса. «Остается животрепещущий вопрос, – писал Эйнштейн коллеге, – распространяется ли понятие относительности до самого конца или может привести к противоречиям». Теперь ученый стремился завоевать главный приз – получить самого большого плюшевого медведя на этом карнавале.

Может ли теория относительности создать модель всей Вселенной?

Это был вопрос в духе интегрирования, переход от «множества маленьких сущностей» к «единому большому всему». На самом деле здесь буквально использовалось интегрирование: хотя в своей знаменитой статье 1917 г. Эйнштейн применяет другой подход, к 1918 г. он обнаружил, что, по существу, берет интеграл. Он предпочел именно такую подачу информации. «У новой формулировки есть одно крупное преимущество, – писал ученый, – в том, что количество… появляется в фундаментальном уравнении как постоянная интегрирования».

Какое количество? Мы до этого еще доберемся. Во-первых, что такое постоянная интегрирования?

Если вы спросите любого студента, изучающего математический анализ, то это раздражающее + С в конце каждого неопределенного интеграла. Эта закорючка используется для удобства обозначений, она не имеет отношения к тому интегралу, который вы вычисляете, но по какому-то непонятному правилу вы никогда не должны о ней забывать во избежание мелочной бюрократии при начислении баллов со стороны преподавателя.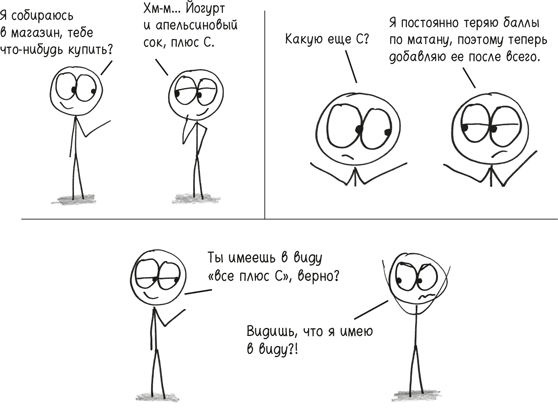

Откуда взялась эта постоянная? Как мы уже обсуждали, интегрирование и дифференцирование – обратные процессы. Чтобы взять интеграл, мы смотрим на функцию и спрашиваем: от чего эта производная?

Представьте себе бегуна, который двигается с постоянной скоростью 7 км/ч. График его скорости будет выглядеть подобным образом: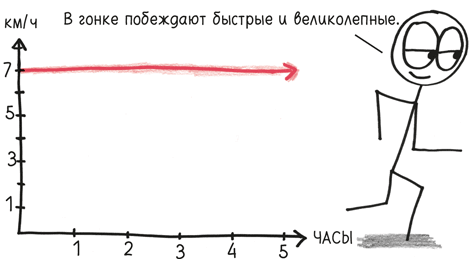

А что насчет интеграла – это будет график местоположения? Вот одна из возможностей: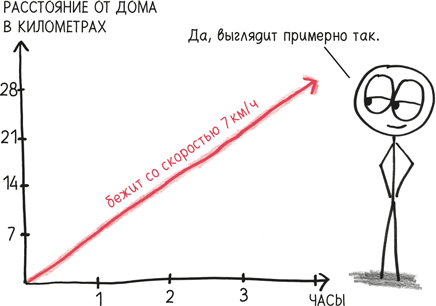

Но это позволяет предположить, что в полдень бегун стартовал из дома. В действительности мы не знаем, где именно началась его пробежка. Возможно, в километре от дома, или в двух, или в семи. Или в трех с половиной, но в противоположной стороне от дома, так что мимо него наш любитель спорта пробежал в половине первого.

Существует бесконечное количество возможных функций положения, которые отличаются только тем, что какое-либо фиксированное расстояние добавляется или убирается. Это может быть 7х, 7х + 1, 7х + 2, 7х + 3…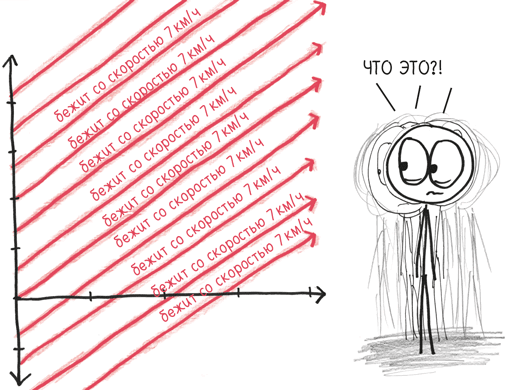

Вместо того чтобы составлять список бесконечных возможностей, из-за которых мы можем опоздать на обед, мы объединяем все семейство функций под простой формулой 7х + С. С – это постоянная интегрирования, сокращение от «любое число, которое придет в голову». Одним махом она трансформирует один-единственный график в бесконечную семью. Из-за ее краткости и лаконичности эту постоянную так легко забыть, но именно «семья» является источником ее силы и глубины.

Нет, Альберт Эйнштейн не забыл о постоянной. Я имею в виду, конечно же, не забыл – мы ведь говорим об одном из величайших ученых, когда-либо отказывавшихся от расчески.

Нет, он допустил гораздо более продуманную ошибку. И она оказалась куда более зрелищной.

«Я должен провести читателя по тому пути, которым прошел сам, – пишет Эйнштейн в статье 1917 г., – по этой достаточно неровной и извилистой дороге». В самом деле, он проводит нас через что-то вроде лабиринта улиц, ведущих только в одном направлении, с препятствиями на каждом математическом повороте. Первая попытка ученого описать всю Вселенную противоречила известным фактам. Вторая потребовала определить особую «правильную» систему координат, что шло вразрез с духом «относительности». А третий путь, предложенный одним из его коллег, «не только не оставлял надежды решить задачу, но, напротив, означал отказ от нее». Его знаменитое уравнение просто не давало Эйнштейну достаточной гибкости.