Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний | Джеффри Уэст | страница 46 | LoveRead.ec

Что же тут происходит? Чтобы это понять, достаточно секундного размышления. В отличие от стен вашей гостиной границы и береговые линии обычно не прямолинейны. Гораздо чаще они бывают изогнутыми, извилистыми линиями, обусловленными местными географическими особенностями или «произвольно» определенными по политическим, культурным или историческим соображениям. Если положить между двумя точками границы или побережья прямую линейку длиной 100 км – а именно это, по сути дела, и делается при топографической съемке, – многие из расположенных между этими точками изгибов и извивов, очевидно, не будут учтены (см. рис. 13). Однако если вместо этого использовать линейку длиной 10 км, это позволит измерить все пропущенные ранее изгибы и извивы, размеры которых превышают 10 км. Более высокое разрешение позволяет рассмотреть более мелкие подробности и более точно проследить извилистые участки, что неизбежно приведет к получению оценки большей, чем была получена при применении более грубой, стокилометровой шкалы. Измерение с шагом 10 км точно так же может не замечать аналогичных изгибов и извивов, размеры которых меньше 10 км; однако их можно учесть, если увеличить разрешение измерений до 1 км, и это снова приведет к увеличению длины. Таким образом, в случае линий, содержащих множество изгибов и извивов, подобно границам и береговым линиям, которые изучал Ричардсон, легко понять, почему при увеличении разрешения их длина систематически растет.

Поскольку этот рост подчиняется простому степенному закону, такие границы на самом деле представляют собой самоподобные фракталы. Другими словами, изгибы и извивы одного масштабного уровня в среднем являются масштабированными копиями изгибов и извивов другого. Поэтому, если вам когда-нибудь казалось, что размытый берег ручейка выглядит в точности как уменьшенная копия размытого берега большой реки или даже как миниатюрная модель Большого каньона, знайте, что вам это не привиделось. Так оно и есть (см. с. 149).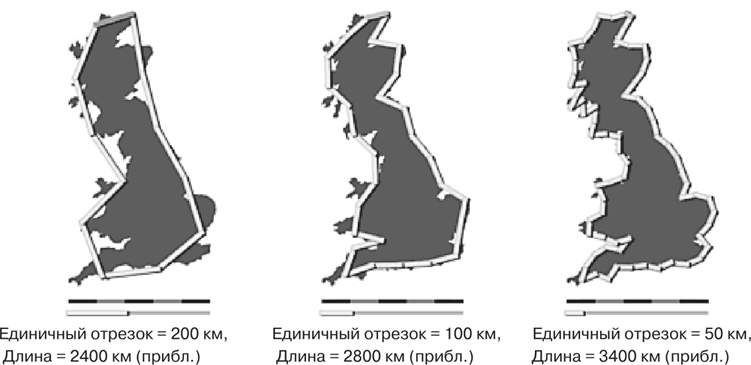

Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний

Рис. 13. Как показывают примеры, длина систематически увеличивается с увеличением разрешения в соответствии со степенным законом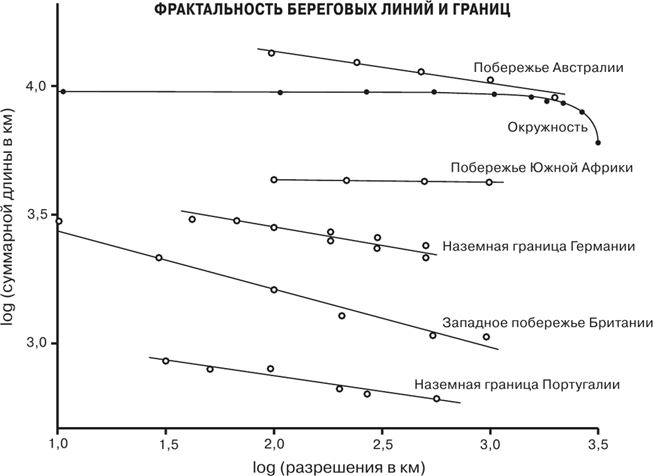

Рис. 14. Наклон зависимости определяет фрактальную размерность берего-вой линии: чем более извилиста эта линия, тем больше наклон

Замечательное открытие. Мы снова видим, что рассмотрение через грубую линзу масштабирования позволяет заметить за головокружительной сложностью мира природы удивительную простоту, регулярность и цельность. Хотя Ричардсон открыл в своих исследованиях границ и побережий это странное, революционное, идущее вразрез со здравым смыслом поведение и даже понял его происхождение, он не осознал его потрясающей всеобщности и далеко идущих следствий. Это, более крупное, открытие совершил Бенуа Мандельброт.

Открытие Ричардсона осталось почти не замеченным научным сообществом. Это и не удивительно, потому что оно было опубликовано в сравнительно малоизвестном журнале, да к тому же и сам Ричардсон был слишком занят своими исследованиями происхождения войн. Его статья, опубликованная в 1961 г., вышла под замечательно невразумительным названием: «Проблема смежности: приложение к статистике смертельных ссор» (The Problem of Contiguity: An Appendix to Statistics of Deadly Quarrels). Даже специалисту было непросто понять из него, о чем идет речь в статье. Кто же мог знать, что эта работа провозглашает важнейшее изменение в нашем мировоззрении?

Понять это смог Бенуа Мандельброт. Ему следует поставить в заслугу не только воскрешение работ Ричардсона, но и осознание их глубокого значения. В 1967 г. он опубликовал во влиятельном журнале Science статью под более понятным названием: «Какова протяженность береговой линии Британии? Статистическое самоподобие и фрактальная размерность»^[69]. Эта работа заново открыла труды Ричардсона, расширив его результаты и обобщив его идеи. Численной мерой морщинистости, которую впоследствии стали называть фрактальностью, был выбран наклон соответствующих прямых на логарифмических графиках Ричардсона: чем круче наклон, тем большей морщинистостью обладает кривая. Величина наклона соответствует показателю степенного закона, связывающего длину с разрешением, аналогичному показателю ¾, который связывает уровень метаболизма с массой организма. Для очень гладких классических кривых, например окружностей, угол наклона – или степенной показатель – равен нулю, так как длина такой кривой не изменяется с увеличением разрешения, а лишь сходится к определенному значению, как в примере с измерением длины гостиной. Однако для неровных, морщинистых береговых линий этот показатель отличен от нуля. Например, для западного побережья Британии он составляет 0,25. Для еще более морщинистых берегов Норвегии с их великолепными фьордами и многоуровневыми заливами и бухтами, которые последовательно разветвляются на все меньшие заливы и бухты, показатель доходит до огромного значения в 0,52. Тем не менее Ричардсон выяснил, что побережье Южной Африки не похоже почти ни на одну другую береговую линию и имеет показатель, равный всего лишь 0,02, близкий к гладкой кривой. Что же касается границы между Португалией и Испанией, «расхождения» длины которой и навели его на эту задачу, ее показатель оказался равным 0,18, см. рис. 14.

Чтобы понять, что означают все эти числа на человеческом языке, представим себе, что разрешение измерений увеличилось в два раза. Тогда, например, измеренная длина западного побережья Британии увеличится приблизительно на 25 %, а побережья Норвегии – более чем на 50 %. Этот сильнейший эффект совершенно не принимался во внимание, пока Ричардсон не наткнулся на него всего семьдесят лет назад. Таким образом, для придания процессу измерения осмысленности совершенно необходимо знать разрешение, являющееся неотъемлемой частью всего этого процесса.

Вывод ясен. В общем случае измеренная длина не имеет смысла, если не указан масштаб разрешения, использованный при ее определении. В принципе, говорить о ней так же бессмысленно, как сказать, что длина равна 543, 27 или 1,289176, не указывая, в каких единицах она измерена. Необходимо знать, какое разрешение было использовано, а также идет ли речь о милях, сантиметрах или ангстремах.

Мандельброт ввел понятие фрактальной размерности, равной сумме 1 и показателя степенного закона (то есть наклона прямой). Так, фрактальная размерность побережья Южной Африки равна 1,02, Норвегии – 1,52 и так далее. Смысл добавления единицы состоит в привязке идеи фракталов к общепринятой концепции обычной размерности, о которой мы говорили в главе 2. Вспомним, что размерность гладкой линии равна 1, размерность гладкой поверхности – 2, а размерность объема – 3. Таким образом, побережье Южной Африки очень близко к гладкой линии, так как его фрактальная размерность, 1,02, очень близка к 1, а побережье Норвегии сильно от нее отличается, поскольку его фрактальная размерность, равная 1,52, значительно больше 1.