Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний - читать онлайн книгу. Автор: Джеффри Уэст cтр.№ 16

Собственно говоря, шкала Рихтера измеряет амплитуду «тряски» при землетрясении, регистрируемую сейсмометрами. Количество выделяющейся при этом энергии масштабируется относительно этой амплитуды нелинейно: при увеличении измеренной амплитуды землетрясения на один порядок выделяющаяся энергия увеличивается на полтора (то есть 3/2) порядка величины. Это означает, что изменение амплитуды на два порядка величины эквивалентно изменению выделяющейся энергии на три порядка (в 1000 раз), а изменение всего на 1,0 балла соответствует изменению энергии в квадратный корень из тысячи, то есть в 31,6 раза ^[29].

Чтобы получить некоторое представление об огромной энергии землетрясений, можно рассмотреть некоторые цифры: при взрыве одного фунта (то есть около 0,5 кг) тринитротолуола высвобождается энергия, приблизительно соответствующая 1 баллу по шкале Рихтера. Сила 3 балла эквивалентна взрыву 1000 фунтов (около 500 кг) ТНТ: взрыв приблизительно такой силы произошел в 1995 г. во время теракта в Оклахома-Сити. 5,7 балла по шкале Рихтера соответствуют приблизительно 5000 т взрывчатки; 6,7 (сила землетрясений в Нортридже и Фукусиме) – приблизительно 170 000 т; 7,7 (землетрясение 2010 г. на Суматре) – приблизительно 5,4 млн т; а 8,7 (землетрясение 2005 г. на Суматре) – приблизительно 170 млн т. Самым сильным из зарегистрированных землетрясений было Великое чилийское землетрясение 1960 г. в городе Вальдивия: его сила составила 9,5 балла (почти в тысячу раз больше по амплитуде, чем в Нортридже и Фукусиме), что соответствует 2700 млн тонн ТНТ.

Отметим для сравнения, что атомная бомба «Малыш», сброшенная в 1945 г. на Хиросиму, высвободила энергию, эквивалентную приблизительно 15 000 тонн ТНТ. Средняя водородная бомба высвобождает более чем в тысячу раз больше энергии, что соответствует крупному землетрясению силой 8 баллов. Речь идет об огромных количествах энергии: 170 млн тонн ТНТ, энергии суматранского землетрясения 2005 г., достаточно для энергоснабжения города с населением 15 миллионов человек (то есть размером со всю агломерацию Большого Нью-Йорка) в течение целого года.

Масштаб, в котором приращение идет не линейно (1, 2, 3, 4, 5…), а по степеням десяти (10¹, 10², 10³, 10⁴, 10⁵…), как на шкале Рихтера, называется логарифмическим. Отметим, что в этом масштабе на самом деле происходит линейное увеличение порядков величины, как видно по показателям степени десяти (верхним индексам). Одна из многочисленных особенностей логарифмического масштаба состоит в том, что она позволяет отображать на одном и том же графике величины, отличающиеся друг от друга по одной из осей во много раз, например силу землетрясения в Вальдивии, землетрясения в Нортридже и взрыва динамитной шашки, то есть значения, различающиеся более чем в миллиард (10⁹) раз. На графике, построенном в линейном масштабе, это было бы невозможно, так как большинство точек сгрудилось бы в самом низу графика. Чтобы построить в линейном масштабе график, включающий в себя все землетрясения, сила которых различается на пять или шесть порядков величины, потребовался бы лист бумаги длиной несколько километров – потому и была изобретена шкала Рихтера.

Благодаря тому что логарифмический масштаб дает удобную возможность компактного представления величин разных порядков на одной и той же странице, он широко используется во всех научных дисциплинах. Эту методику, позволяющую охватить сразу весь диапазон сильно изменяющихся величин, широко применяют, например, для представления яркости звезд, кислотности химических растворов (величины рН), физиологических характеристик животных или ВВП разных стран мира. Именно так построены графики, приведенные на рис. 1–4 во вступительной главе.

Важная особенность науки, часто отличающая ее от других умственных занятий, состоит в требовании подтверждения гипотез опытами и наблюдениями. Это вовсе не тривиальное обстоятельство, как можно видеть из того факта, что утверждение Аристотеля, согласно которому скорость предметов, падающих под действием силы тяжести, пропорциональна их весу, никто не удосужился проверить в течение более двух тысяч лет, а когда его наконец проверили, оно оказалось ошибочным. К сожалению, хотя многие из наших нынешних догм и убеждений, особенно в ненаучных областях, точно так же остаются непроверенными, в них безоговорочно верят, даже не пытаясь найти им каких-либо подтверждений – и это порой приводит к неприятным и даже катастрофическим последствиям.

Поэтому, завершив наше отступление, посвященное степеням десяти, я хотел бы приложить то, что мы узнали о порядках величины и логарифмах, к проверке предсказаний Галилея относительно масштабирования прочности или силы при изменении массы. Можно ли показать, что в «реальном мире» сила действительно изменяется с массой так, как предсказывает правило, гласящее, что изменение порядка ее величины должно происходить в пропорции два к трем?

В 1956 г. химик М. Г. Лицке придумал простое и элегантное подтверждение предсказания Галилея. Он осознал, что данные о том, как максимальная сила масштабируется при изменении массы тела, по меньшей мере у человека, можно найти в статистике тяжелоатлетических соревнований в разных весовых категориях. Все лучшие тяжелоатлеты стараются максимально увеличить вес, который они могут поднять, и тренируются для этого приблизительно с одинаковой интенсивностью и в течение одинакового времени, что позволяет сравнивать их силу в приблизительно одинаковых условиях. Кроме того, соревнования проводятся в трех дисциплинах – жим, рывок и толчок, – так что совокупные результаты по всем трем достаточно хорошо усредняют индивидуальные вариации склонности к той или иной из этих дисциплин. Поэтому такие суммарные результаты можно считать хорошей мерой максимальной силы.

Используя суммарные результаты по всем трем дисциплинам тяжелоатлетических соревнований на Олимпийских играх 1956 г., Лицке блестяще подтвердил, что сила масштабируется с массой тела по степенному закону с показателем, равным ⅔. Результаты всех обладателей золотых медалей были нанесены на график зависимости от веса их тела в логарифмическом масштабе, то есть по каждой оси были отложены приращения в десять раз. Если сила, отложенная по вертикальной оси, увеличивается на два порядка при каждом увеличении массы тела, отложенной по горизонтальной оси, на три порядка, то график должен представлять собой прямую, наклон ^[30] которой равен ⅔. Результат измерений Лицке был равен 0,675, что чрезвычайно близко к предсказанному значению (⅔ = 0,667). Его график приведен на рис. 7 ^[31].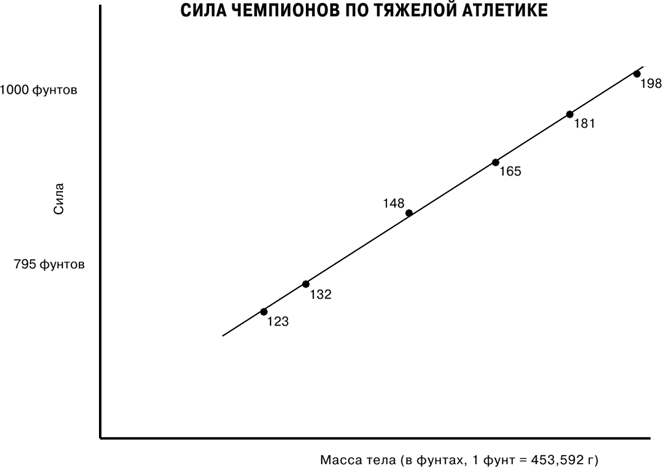

Рис. 7