Футболоматика - читать онлайн книгу. Автор: Дэвид Самптер cтр.№ 9

Ответ. Решение для пяти и шести точек.

Давайте сделаем проблему соединения пригородов действительно сложной. Попробуем решить эту проблему, если мы не знаем расположения пригородов или даже сколько их необходимо подключить. С такой проблемой постоянно сталкивается слизевик под названием Physarum polycephalum. Слизевики не имеют мозга и состоят всего из одной клетки. Их «тело» представляет собой сеть взаимосвязанных трубок, которые качают питательные вещества назад и вперед. Слизевиков можно обнаружить на лесной подстилке или деревьях. Обычно они покрывают площадь меньше монеты, однако они могут сжиматься в неблагоприятных условиях и разрастаться, если еды вдоволь.

Когда слизевики ищут еду, они решают проблему соединения пригородов. Вдохновленный этой идеей, мой японский коллега Тоси Накагаки решил проверить, смогут ли слизевики создать сеть метрополитена и скоростного трамвая Токио. Он и его коллеги разложили питание слизевиков в виде масштабной модели Большого Токио. Они положили овсяные хлопья в чашки Петри: одна большая посередине как отображение центра города и поменьше в местах, соответствующих Сибуе, Иокогаме, аэропорту в Тибе и другим близлежащим районам. Чтобы добиться соединения чашек с овсом, слизевики должны решить ту же проблему, которую разрешили японские градостроители при проектировании транспортной системы Токио. Могут ли слизевики формировать эффективные связи между своими продовольственными ресурсами?

Эксперименты прошли отлично ^[14]. Создать сеть треугольников, соединяющих овсяные хлопья, не составило им труда. Тоси сравнил решение слизевиков с реальной транспортной сетью в Токио и обнаружил, что, хотя они и не были идентичными, у них была схожая структура. Решение слизевиков было так же эффективно, как и специалистов по городскому планированию; помимо этого, они использовали близкое к реальному число связей для объединения овсяных хлопьев. Сравнение решений слизевиков и людей показано на рисунке 2.3.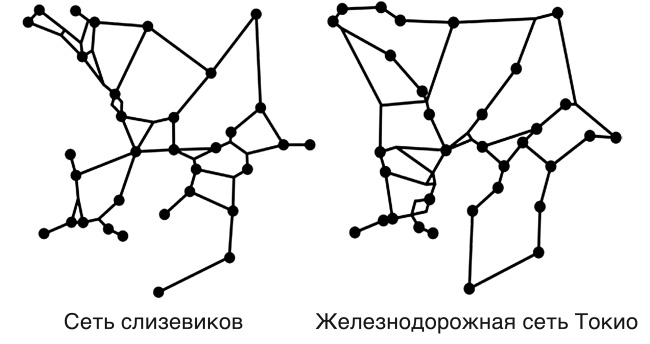

Рисунок 2.3. Сравнение сети, построенной слизевиками для объединения овсяных хлопьев (круги), расположенных в соответствии с пригородами Токио (слева), и реальной железнодорожной сети (справа). Воспроизводится с разрешения Американской ассоциации содействия развитию науки.

Соединения треугольников – главная особенность трубчатых сетей слизевиков. Некоторые овсяные хлопья становятся узлами, которые соединяются с другими точками, так что общая длина трубок остается небольшой.

Обратите внимание: углы в этих узловых пунктах велики, как и в футбольных схемах, и сеть распространяется равномерно во всех направлениях. Слизевики не строят наименьшую возможную сеть для объединения овсяных хлопьев: они создали несколько петель, обеспечив различные способы перемещения между одними и теми же точками. Тоси и его коллеги объяснили, что эти петли очень полезны, если структура повреждена или разрушена. Если одно звено в сети разорвано, слизевик все равно остается связанным и может передавать ресурсы по альтернативному маршруту. Это похоже на ситуацию с аварией на одном отрезке ветки метро. Если система хорошо спроектирована, то не придется отключать всю сеть из-за поломки на одной ветке.

Сети слизевиков и железнодорожных служб по конструкции существенно отличаются от футбольных построений. Футбольные команды не размечают линии передач с помощью трубок или рельсов – они просто пасуют друг другу. Но есть и несколько повторяющихся сходств. Во-первых, идея покрыть треугольниками весь мир. Слизевики покрывают небольшую площадь лесной подстилки, «Барселона» заполняет поле потенциальными передачами, а хорошая железнодорожная служба связывает страну железнодорожными магистралями.

Еще одно важное сходство состоит в том, что между различными вариантами в связующих узлах лежат большие углы. Если мы поворачиваем на 360° вокруг центральных точек сети слизевиков или железных дорог, мы обнаруживаем, что во всех направлениях есть равномерно расположенные варианты – как мы видели в «Барселоне».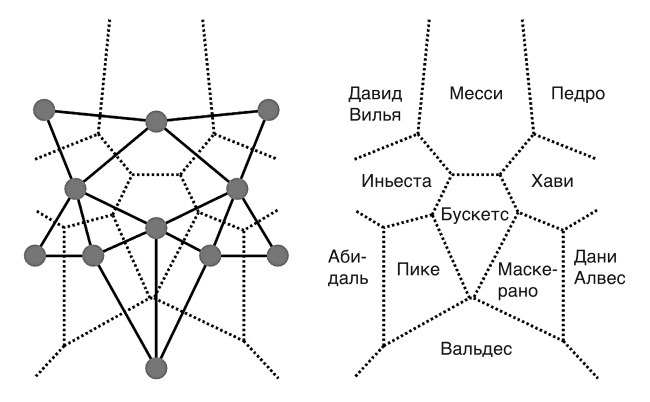

Рисунок 2.4. Сеть и зоны «Барселоны» в сезоне-2010/11. Сеть расположения (сплошные линии) вместе с зонами (пунктирные линии) для каждого игрока (слева); типичная позиция для каждого игрока в течение сезона (справа).

Существует математическая связь между сетями с широким треугольником и эффективным использованием пространства. Схемы разбивки на треугольники, которые я построил, могут быть использованы также для того, чтобы рассмотреть, как команда делит поле на зоны ^[15]. Полученные для «Барселоны» зоны показаны на рисунке 2.4. Слева – сеть игроков и созданные ею зоны (пунктирные линии). Справа я убрал сеть, оставив только зоны, и добавил игроков, которые были в каждой из зон в сезоне-2010/11.

Тот факт, что мозаика зон в схеме 4–3–3 «Барселоны» своей симметричной красотой похожа на сеть их передач, не случаен – это математическая необходимость.

Когда команда строит сеть с широкоугольными треугольниками, она также разделяет область на просторные зоны. Аналогично если каждый игрок занимает точно определенную позицию, то образовывается широкоугольная сеть треугольников ^[16]. Этот момент имеет решающее значение: он говорит нам, что решение одной проблемы даст нам решение и для второй. Если команда хорошо занимает пространство, игроки найдут много удачных возможностей отдать пас. Если они открываются для получения паса, они поймут, что создали свободное пространство. Игрокам не нужно вычислять все углы к своим партнерам – они просто должны убедиться, что у них достаточно места, чтобы принять мяч и сделать передачу.