Укрощение бесконечности. История математики от первых чисел до теории хаоса - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 70

Чтобы составить такую схему, мы расположим по одной вершине на каждом массиве суши: северный берег, южный берег и два острова. Соединим две вершины ребром всякий раз, когда есть мост, связывающий соответствующие фрагменты суши. Тогда мы получаем четыре вершины A, B, C и D и семь ребер, по одному для каждого моста.

Теперь задачу можно заменить более простым эквивалентом на схеме. Возможно ли найти на ней маршрут – связанную последовательность ребер, чтобы он включал по одному разу каждое ребро?

Эйлер определил два типа маршрутов: открытый, у которого начало и конец находятся в разных вершинах, и замкнутый, у которого начало и конец приходятся на одну вершину. Он доказал, что именно для этой схемы не существует маршрута ни одного из этих типов.

Ключом к загадке станет рассмотрение валентности каждой вершины: в данном случае это число сходящихся в ней ребер. Сперва рассмотрим вариант замкнутого маршрута. Здесь каждое ребро, приходящее к вершине, соединяется с другим – следующим, по которому маршрут покидает эту вершину. Если замкнутый маршрут возможен, количества ребер для каждой вершины должны, соответственно, быть четными. Иными словами, у всех вершин должна быть равная валентность. Но на схеме мы видим три вершины с валентностью 3 и одну с валентностью 5 – всё это нечетные числа. Значит, замкнутого маршрута не существует.

Те же критерии мы применяем к открытому маршруту, но здесь получится минимум две вершины с нечетной валентностью: одна в начале и другая в конце. Поскольку на схеме Кенигсберга есть четыре вершины с нечетной валентностью, открытого маршрута не существует.

Эйлер сделал еще один важный шаг – доказал, что эти необходимые условия для существования маршрута являются также достаточными при условии, что на диаграмме есть связь (т. е. две любые вершины связаны каким-либо путем). Это общее свойство доказать несколько труднее, и у Эйлера ушло некоторое время на поиски решения. Сейчас мы можем записать доказательство в нескольких строках.

Два открытия Эйлера кажутся принадлежащими к весьма далеким друг от друга разделам математики, но при внимательном рассмотрении легко заметить общие для них детали. Они используют комбинаторику схем многогранников. Одно считает грани, ребра и вершины, а другое – валентности; одно выводит общие соотношения между тремя числами, другое ищет что-то общее в имеющихся маршрутах. Но они явно родственны по духу. И даже больше, причем эта особенность оставалась незамеченной на протяжении более чем столетия: оба являются инвариантами непрерывных преобразований. Само расположение вершин и ребер здесь не имеет значения: нам важно лишь то, как они связаны между собой. Обе проблемы покажутся одинаковыми, если мы нарисуем эту схему на резиновом листе, который потом деформируется. Единственный способ создать значимые различия – разрезать или разорвать этот лист и склеить потом его куски; но эта операция уничтожит саму непрерывность.

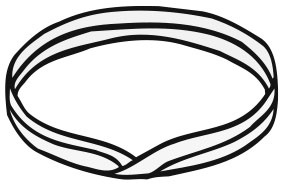
Проблески общей теории первым заметил Гаусс, время от времени пытавшийся привлечь внимание коллег к необходимости некой теоретической базы для геометрических свойств схем. Он также изобрел новый топологический инвариант, который мы сейчас называем коэффициентом зацепления, для исследований магнетизма. Это число определяет, как одна замкнутая кривая обкручивается вокруг другой. Гаусс вывел формулу для подсчета коэффициента зацепления на основе аналитических выражений, описывающих кривые. Такой же инвариант, число оборотов (или индекс точки) для замкнутой кривой по отношению к точке, был использован в одном из доказательств Основной теоремы алгебры.

Наибольший вклад в становление топологии внесли студент Гаусса Иоганн Листинг и ассистент Август Мёбиус. Листинг учился у Гаусса в 1834 г., и в его труде «Предварительные исследования по топологии» впервые используется термин «топология». Сам Листинг сначала применял выражение «геометрия позиций», но его уже пустил в обиход Карл фон Штаудт для описания проективной геометрии, и Листингу пришлось искать другой вариант. Кроме того, Листинг искал способ обобщения формулы Эйлера для многогранников.

Мёбиус сумел четко обозначить важную роль непрерывных преобразований. Его нельзя было назвать самым продуктивным ученым, но он отличался чрезвычайно кропотливым подходом к любой исследуемой им теме. В частности, именно он обратил внимание на то, что у поверхности отнюдь не всегда есть две четко разделенные стороны, приведя в пример свою знаменитую ленту. Эту поверхность независимо друг от друга открыли и Мёбиус, и Листинг в 1858 г. Листинг опубликовал свое открытие в книге «Der Census Räumlicher Complexe» («Описание пространственной сложности»), а Мёбиус – в статье об исследовании свойств поверхностей.

Долгое время идеи Эйлера о многогранниках оставались в стороне от основных направлений математической мысли, но в какой-то момент несколько маститых ученых открыли новый подход к геометрии, который они назвали тогда analysis situs, т. е. анализ размещений. Под этим подразумевалась качественная теория форм как самостоятельная дисциплина, дополняющая более привычную тогда количественную теорию длин, углов, площадей и объемов. Этот взгляд делался всё более популярным по мере появления новых открытий в традиционных исследованиях основных направлений математики. Ключевым шагом стало открытие связей между комплексным анализом и геометрией поверхностей, сделанное Риманом.

Очевидный способ осмысления комплексной функции f состоит в том, чтобы интерпретировать ее как отображение из одной комплексной плоскости в другую. Базовая формула для такой функции, w = f(z), предлагает нам взять любое комплексное число z, применить к нему f и получить другое комплексное число w, связанное с z. Геометрически z принадлежит одной комплексной плоскости, а w – фактически второй, независимой копии комплексной плоскости.