Укрощение бесконечности. История математики от первых чисел до теории хаоса - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 69

В 1639 г. Декарт отметил любопытную черту нумерологии правильных тел. Взять, к примеру, куб. Это 6 граней, 12 ребер и 8 вершин. Сложите 8 и 6, и вы получите 14, на 2 больше, чем 12. А как насчет додекаэдра? У него 12 граней, 30 ребер и 20 вершин. И 12 + 20 = 32, что на 2 больше 30. То же повторяется у тетраэдра, октаэдра и икосаэдра. Та же особенность, судя по всему, присуща практически всем многогранникам. Если тело имеет F граней, Е ребер и V вершин, то F + V = E + 2, что можно переписать как

F – E + V = 2.

Декарт не опубликовал свое открытие, но записал его в своем манускрипте, прочитанном Лейбницем в 1675 г.

Эйлер первым опубликовал это соотношение в 1750 г. Он добавил доказательство в 1751 г. Его увлекли эти взаимоотношения, потому что он пытался разработать классификацию многогранников. В работе над классификацией ученому приходится учитывать любое общее свойство предметов, подобное этому.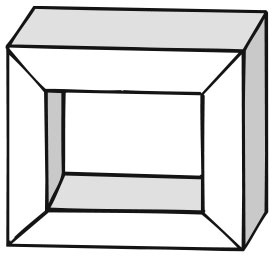

Многогранник с отверстием

Существует ли формула, верная для всех многогранников? Не совсем так. Если наш многогранник имеет форму рамы для картины, с квадратным поперечным сечением и прямыми углами, то у него 16 граней, 32 ребра и 16 вершин, т. е. здесь F + V – E = 0. Причиной такого несоответствия оказывается наличие отверстия. Фактически если многогранник имеет g отверстий, то

Что же это – отверстие? Ответ найти труднее, чем кажется. Во-первых, речь идет о поверхности многогранника, а не о его сплошном внутреннем пространстве. В реальной жизни для того, чтобы сделать отверстие в чем-либо, мы внедряемся в его твердую сплошную внутренность, но приведенные выше формулы не имеют отношения к ней – только к граням, образующим его поверхность, заодно с их ребрами и вершинами. Всё, с чем мы имеем дело, лежит на поверхности. Во-вторых, единственный вид отверстий, влияющий на численные данные, – те, что пронзают тело насквозь, образуя туннель с двумя концами. Проще говоря, это не такое отверстие, которое может вырыть рабочий на дороге. В-третьих, такие отверстия могут не быть на поверхности, хотя отчасти именно поверхности очерчивают их. Отверстие существует только в качестве пустого места в бублике, но даже в этом случае вы покупаете твердую внутренность бублика.

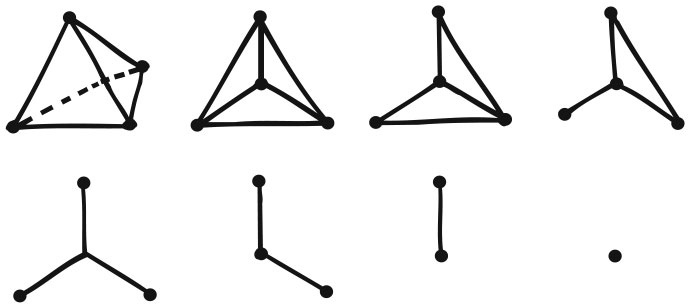
Пример доказательства Коши

Наверное, проще исходить из определения, что значит «не отверстие». Многогранник не имеет отверстий, если его можно непрерывно деформировать, получая искривленные грани и ребра, пока он (вернее, его поверхность) не превратится в сферу. Для таких поверхностей F + V – E на самом деле всегда будет равно 2. И обратное утверждение верно: если F + V – E = 2, многогранник можно деформировать в сферу.

Непохоже, что многогранник в виде рамы для картины можно деформировать в сферу, – куда же денется отверстие? Для строгого доказательства этого мы не должны заглядывать дальше того факта, что для этого многогранника F + V – E = 0. Такое соотношение невозможно для поверхностей, способных деформироваться в сферу. Итак, числа многогранников описывают для нас важные особенности их геометрии, и последние могут быть топологическими инвариантами – неизменными при деформациях.

Сейчас формула Эйлера кажется нам замечательным намеком на очень полезную связь между комбинаторными аспектами многогранника, такими как количество граней, и его топологическими аспектами. Получается, что проще двигаться в обратном направлении.

Чтобы вычислить количество отверстий на поверхности, возьмем F + V – E – 2, разделим на 2 и изменим знак:

Курьезный вывод: теперь мы можем вычислить количество отверстий в многограннике, не давая определения отверстия.

Преимущество такой процедуры в том, что она естественна для многогранника, не требует визуального контакта с ним в окружающем трехмерном пространстве – того, как видят отверстие наши глаза. Необычайно разумный муравей, обитающий на поверхности многогранника, может решить, что там есть какое-то отверстие, даже если видит только поверхность. Эта естественная точка зрения присуща топологии. Она изучает форму предметов как таковую, саму по себе, а не как часть чего-то еще.

На первый взгляд задача о кенигсбергских мостах не имеет отношения к комбинаторике многогранников. Город Кенигсберг (ныне Калининград), некогда принадлежавший Пруссии, расположен по обоим берегам реки Преголя, на которой есть два острова. Те связаны с берегами и друг с другом семью мостами. Понятно, что жители Кенигсберга долго гадали, можно ли так проложить маршрут воскресной прогулки, чтобы только один раз пройти по каждому из мостов.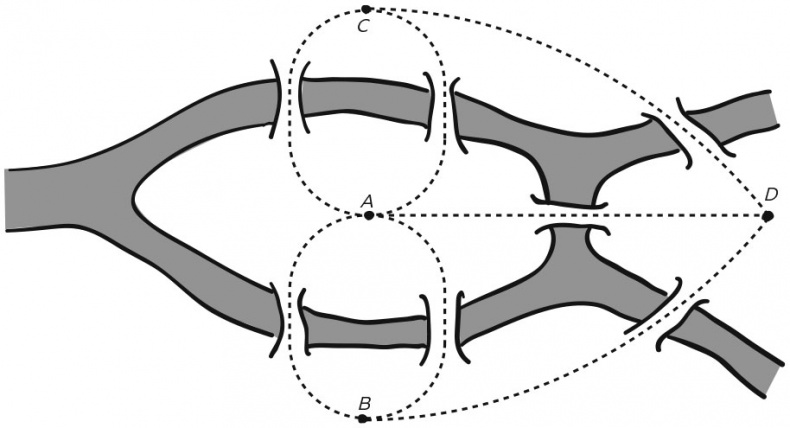

Задача о кенигсбергских мостах

Загадку в 1735 г. решил Эйлер; хотя правильнее будет сказать, он доказал, что здесь нет решения, и объяснил почему. Он использовал два важных приема: упростил задачу и сократил ее до самых элементарных требований, а затем обобщил ее, сравнив со всеми головоломками такого рода. Он указал, что для решения важны не размеры и форма островов, а то, как именно связаны между собой острова, берега и мосты. Всю проблему можно было изобразить простой схемой точек (вершин), соединенных линиями (ребрами), как это показано наложением на нашей карте.