
|
||
|
|
||
|
|
Онлайн книга - Укрощение бесконечности. История математики от первых чисел до теории хаоса | Автор книги - Йен Стюарт
Cтраница 45

Примерно в 1830 г. Майкл Фарадей занялся экспериментами по электричеству и магнетизму, исследуя возникновение магнитного поля под воздействием электрического тока и появление электрического поля при движении магнита. Современные генераторы и электромоторы – прямые потомки сконструированных им аппаратов. В 1864 г. Джеймс Клерк Максвелл преобразовал выкладки Фарадея в математические уравнения, описывающие электромагнетизм, – уравнения Максвелла. Это были ДУЧП, относившиеся к явлениям электричества и магнетизма. Простой вывод из уравнений Максвелла приводит нас к волновому уравнению. Этот расчет показывает, что электрическое и магнитное поля могут передвигаться вместе, подобно волне, со скоростью света. А что движется с такой скоростью? Свет! А значит, свет – электромагнитная волна. Уравнение не ставит пределов для частоты волны, световые волны демонстрируют сравнительно небольшой диапазон частот. Из этого физики заключили, что должны существовать и другие электромагнитные волны с иными частотами. Генрих Герц продемонстрировал физическое существование таких волн, а Гульельмо Маркони обратил их к практической пользе, создав радио. Дальше число новых технологий стало расти как снежный ком. Телевизор и радар также работают на электромагнитных волнах, как и спутниковая навигационная система GPS, сотовые телефоны и беспроводные компьютерные сети. 
Радиоволны Физика становится математической
Невозможно переоценить значение для науки «Начал» Ньютона, заложивших математическую основу в описание самых сложных природных явлений. Но последующие события оказались не менее важными. Математики взялись за исследование всего, что прежде считалось предметом изучения физики: звука, тепла, света, гидродинамики, притяжения, электричества, магнетизма. И для всех этих явлений они вывели дифференциальные уравнения, поразительно точно описывавшие законы физики. Еще более поразительными стали дальнейшие шаги науки. Множество самых выдающихся технических достижений, таких как изобретение радио и телевидения и обеспечение воздушных перевозок, зависело от математики дифференциальных уравнений. И эта область остается одной из наиболее активно развивающихся в науке, где практически каждый день совершаются новые открытия. Не будет преувеличением сказать, что изобретение Ньютоном дифференциальных уравнений, получивших практическое приложение благодаря его последователям в XVIII−XIX вв., во многом определило облик современного мира. Это очевидно, если вы дадите себе труд заглянуть за кулисы сегодняшней жизни. Глава 10. Невозможные величины
Квадратные корни отрицательных чисел: возможно ли? Математики различают несколько видов чисел с разными свойствами. Главное здесь не отдельные числа, а «сообщество», к которому они принадлежат, – иными словами, то, с кем они водят компанию. Четыре из этих систем чисел хорошо нам знакомы: натуральные: 1, 2, 3, …; целые, куда также входит 0 и отрицательные не дробные; рациональные, включающие дроби вида p/q, где p и q – целые числа, причем q не равно 0; и действительные числа, обычно представляемые десятичными дробями с бесконечным количеством знаков после запятой – что бы это ни значило. Они включают рациональные числа, в том числе периодические десятичные дроби, и иррациональные, такие как √2, e и π, у которых в цифрах после запятой нет повторяющихся последовательностей. Целые числа
Само название подразумевает нечто единое; остальные создают впечатление, что упомянутые системы представляют собой некие ощутимые, действительные вещи: натуральные, рациональные и, конечно, вещественные. Эти названия отражают и в то же время поддерживают давно сложившееся мнение, что числа – неотъемлемая черта окружающего нас мира. Многие уверены, что единственный способ сделать открытие в математике – изобрести новые числа. И это убеждение ложно: многие разделы математики вообще не имеют дела с числами, и, во всяком случае, цель любого исследования – изобретение новых теорем, а не чисел. Однако порой появляются и «новые числа». И одно из таких изобретений – «невозможное», или «мнимое», число – коренным образом изменило облик математики, наделив ее поистине невероятной мощью. Этим числом стал квадратный корень из –1. Древним математикам сама эта идея показалась бы чушью, потому что в их времена квадрат любого числа мог быть только положительным. А значит, отрицательные числа не могут иметь квадратных корней. Но попробуйте представить, что они есть. Что тогда будет? Математикам понадобилось очень много времени, чтобы понять: числа – не более чем искусственно созданные изобретения человеческого разума. Они незаменимы для постижения окружающего мира, но в то же время являются его частью не более, чем любой из треугольников Евклида или вычислительная формула. На протяжении истории нашей культуры математики противились этой философской проблеме, пока не убедились, что мнимые числа незаменимы, полезны и даже в чем-то схожи с более привычными нам действительными. Проблемы с кубическим уравнением
Революционные идеи в математике редко зарождаются в простом и на поверку очевидном контексте. Чаще всего им необходима сложная почва. Так вышло с квадратным корнем из –1. Сейчас мы обычно вводим это число в квадратном уравнении x2 + 1 = 0, решением для которого становится √–1 – что бы это ни значило. Первыми математиками, задавшимися вопросом, имеет ли это хоть какой-то смысл, стали алгебраисты эпохи Возрождения, пришедшие к проблеме квадратных корней из отрицательных чисел несколько необычным путем: в поисках решений для кубических уравнений. Вспомним, как дель Ферро и Тарталья нашли решение для кубических уравнений, позже опубликованных Кардано в его труде «Великое искусство». В современных символах решение для кубического уравнения x3 + ax = b выглядит так: 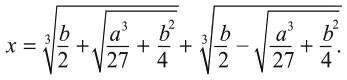
Математики эпохи Возрождения описали это выражение словами, но методика вычислений была точно такой же. Иногда эта формула работает безупречно, но порой чревата проблемами. Кардано заметил, что, когда формулу применяют к уравнению x3 = 15x + 4, с явным решением x = 4, результат выглядит так: 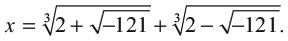
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно