Укрощение бесконечности. История математики от первых чисел до теории хаоса - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 34

Cтраница 34

Ситуация кардинально изменилась, когда за дело взялся Гаусс и открыл общие концептуальные основы теории чисел, такие как модульная арифметика. Также своими исследованиями свойств правильных многоугольников он связал теорию чисел с геометрией. С этого момента теория чисел превратилась в заметную нить на пестром ковре математики.

Интуиция Гаусса привела математиков к открытию принципиально новых структур – новых числовых систем, таких как целые числа по mod n, а также математических действий, таких как композиция квадратичных форм. Благодаря новым открытиям теория чисел конца XVIII – начала XIX в. породила абстрактную алгебру конца XIX – начала XX в. Математики уже не боялись выходить за рамки привычных концепций и структур в своих исследованиях. Несмотря на узкоспециализированную тему, «Арифметические исследования» стали значительной вехой на пути создания современного подхода к математике в целом. И это одна из причин, почему математики так высоко оценивают роль Гаусса.

Вплоть до конца XX в. теория чисел пребывала в рамках чистой математики – любопытная сама по себе, с многочисленными способами приложения к собственно математическим исследованиям. Но она всё еще не играла особой роли для остального мира. Однако всё изменилось с момента изобретения цифровой связи в конце XX в. Как только она стала полностью зависеть от чисел, теория чисел предсказуемо оказалась на переднем крае. Чтобы хорошая математическая идея обрела практическое значение, могут уйти годы – а иногда даже сотни лет, – но рано или поздно любая область, некогда считавшаяся важной только среди математиков, находит дорогу в реальный мир и занимает там подобающее ей место.

Изобретение исчисления

Хотя Лейбниц скорее мог бы претендовать на первенство в открытии исчисления, Ньютон превратил его в главную технику зарождающейся отрасли науки – классической физики, позже ставшей главным инструментом в познании человечеством мира природы. Сам Ньютон назвал свою теорию «Система мира». Пожалуй, звучит не очень скромно, зато точно определяет предмет. До Ньютона представления людей о законах природы в основном исходили из идей Галилея о движении тел, в частности параболической траектории полета пушечного ядра, а также открытой Кеплером эллиптической формы орбиты Марса в небесах. После Ньютона математические формулы пронизали почти все области физического мира: движение земных и небесных тел, потока воздуха и воды, передачи тепла, света, звука, силу тяготения.

Тем более любопытно, что в главном опубликованном Ньютоном труде, «Математические начала натуральной философии», исчисление не упоминается вообще. Он посвящен изящному применению геометрии в стиле, заданном древними греками. Но внешность порой обманчива: неопубликованные документы, известные как «Портсмутские бумаги», доказывают, что во время работы над «Началами» Ньютон сформировал представление об идее исчисления. Очень похоже, что ученый использовал методы исчисления в большинстве своих открытий, однако предпочел не распространяться о них. Его наработки были опубликованы уже после его смерти, в книге «Метод флюксий и бесконечных рядов», в 1732 г.

Что такое исчисление? Метод, изобретенный Ньютоном и Лейбницем, проще понять, ознакомившись с более ранними идеями. Исчисление – это математика мгновенных изменений: насколько быстро изменяется определенная величина в это самое мгновение. Вот пример из физики: поезд движется по рельсам; как быстро он едет прямо сейчас? Исчисление делится на две главные ветви. Дифференциальное исчисление обеспечивает методы измерения скорости изменений и в большинстве случаев приложимо к геометрии, в частности при нахождении касательных к кривым. Интегральное исчисление подразумевает противоположное действие: исходя из скорости изменения некой величины, оно позволяет найти саму величину. Геометрические приложения интегрального исчисления включают способы вычисления площадей и объемов. Пожалуй, самым значительным открытием как раз и стала эта неожиданная связь между двумя внешне независимыми геометрическими вопросами: нахождение касательных к кривым и нахождение площадей.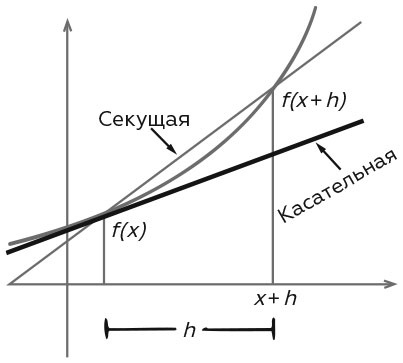

Геометрический смысл производной

Исчисление неразрывно связано с функциями – действиями, когда берется некое исходное число и определяется другое, связанное с ним. Как правило, такое действие описывается формулой, где данному числу, обозначенному как x (возможно, с некими дополнительными условиями), вводится в соответствие число f(x). В качестве примеров можно привести функцию квадратного корня f(x) = √x (в этом случае x должно быть неотрицательным числом) и квадратную функцию f(x) = x² (в этом случае для x нет никаких условий).

Первой ключевой идеей исчисления является дифференцирование, т. е. взятие производной функции. Производная – это скорость изменения функции f(x), сравниваемая с изменением x, т. е. скорость изменения f(x) относительно x.

Геометрически скорость изменения – это тангенс угла наклона графика f в точке х. К нему можно приблизиться, определив угол наклона секущей – линии, пересекающей график в двух наиболее близких точках, соответствующих x, и x + h, где h невелико. Угол наклона секущей равен: