Укрощение бесконечности. История математики от первых чисел до теории хаоса | Йен Стюарт | страница 32 | LoveRead.ec

Публичная репутация Гаусса, несмотря на это, опирается на астрономическое предсказание. В 1801 г. Джузеппе Пиацци открыл первый астероид – Цереру. Его наблюдения были столь неполны, что астрономы боялись не найти небесное тело снова, когда то покажется из-за Солнца. Поэтому многие астрономы взялись предсказать, где Церера появится вновь, в том числе Гаусс. Но прав оказался только он. Фактически Гаусс воспользовался методом, ставшим возможным благодаря его открытию, которое известно в наши дни как метод наименьших квадратов и позволяет получить точные результаты в условиях ограниченных наблюдений. Ученый не опубликовал в свое время этот метод, хотя в итоге он лег в основу статистики и наблюдательных исследований.

В 1805 г. Гаусс женился на Иоганне Остгоф, которую горячо любил, а в 1807 г. перебрался из Брауншвейга в Гёттинген, где стал директором обсерватории. В 1808 г. скончался его отец, следом в 1809 г. родами второго сына умерла Иоганна, а вскоре и их новорожденный малыш.

Несмотря на все эти личные трагедии, Гаусс продолжил исследования и в 1809 г. опубликовал «Теорию движения небесных тел, движущихся в конических сечениях вокруг Солнца», в которой есть положения, до сих пор лежащие в основе вычислений небесной механики. Он женился снова на подруге Иоганны, Минне, но это был брак не по любви, а скорее по расчету.

Примерно в 1816 г. Гаусс составил обзор умозаключений из аксиомы параллельности, отличной от других аксиом Евклида, в которых он придерживается точки зрения, скорее всего, появившейся еще в 1800 г.: о возможности существования логически обоснованной геометрии, отличной от евклидовой.

В 1818 г. ему поручили провести геодезическую съемку Ганновера, в ходе которой он сделал несколько значительных вкладов в методы геодезии. В 1831 г., после кончины Минны, Гаусс вместе с физиком Вильгельмом Вебером приступил к изучению магнитного поля Земли.

Он открыл законы, известные нам как правила Кирхгофа для электрических цепей, и даже собрал пусть и неуклюжий, но вполне работоспособный телеграф. Когда в 1837 г. Веберу пришлось покинуть Ганновер, научная активность Гаусса пошла на спад, хотя он продолжал интересоваться трудами коллег, особенно Фердинанда Эйзенштейна и Георга Бернхарда Римана. Гаусс мирно скончался во сне.

Ответ на этот вопрос лежит в области простых чисел. Если p и q – простые числа, когда q является квадратом по mod p? Гаусс открыл, что если нет способа просто и прямо ответить на этот вопрос, то можно задать другой, имеющий прямое отношение к предыдущему: когда p является квадратом по mod q? Например, приведенный выше перечень квадратичных вычетов показывает, что q = 5 является квадратом по модулю p ≡ 11. Также верно и то, что 11 является квадратным модулем 5, потому что 11 ≡ 1 (mod 5) и 1 ≡ 1². В общем, ответ на оба вопроса один.

Гаусс доказал, что его квадратичный закон взаимности справедлив для любой пары случайно взятых нечетных простых чисел, за исключением тех вариантов, когда оба можно описать как 4k – 1. Тогда на два вопроса есть два противоположных ответа. Например: для любых случайно взятых простых чисел p и q второе число есть квадрат по mod p тогда и только тогда, когда p есть квадрат по mod q, в случае, если p и q не описываются формулой 4k – 1. Иначе q есть квадрат по mod p тогда и только тогда, когда p не есть квадрат по mod q.

Поначалу Гаусс не подозревал, что это не первое утверждение такого рода: Эйлер уже успел отметить ту же зависимость. Но, в отличие от Эйлера, Гаусс сумел доказать, что оно всегда верно. Доказательство оказалось крайне сложным, и у Гаусса ушло несколько лет на то, чтобы ликвидировать эту небольшую, но ключевую брешь.

ЧТО ТЕОРИЯ ЧИСЕЛ ДАЛА ИМ

Одним из самых ранних применений теории чисел являются шестерни. Если два зубчатых колеса помещены так близко, что зубцы одного входят между зубцами другого, причем у одного m, а у другого n зубцов, то их совместное движение будет зависеть от этих чисел. Например, пусть у одного колеса 30 зубцов, а у другого семь. Если большое колесо совершит ровно один полный поворот, что будет с меньшим? Оно будет возвращаться в исходную позицию после 7, 14, 21 и 28 шагов. Тогда ему потребуются еще два завершающих шага до полных тридцати. Это число – остаток, который получается при делении 30 на 7. Значит, движение колес является механическим воплощением примера на деление с остатком, это и есть основа модульной арифметики.

Укрощение бесконечности. История математики от первых чисел до теории хаоса

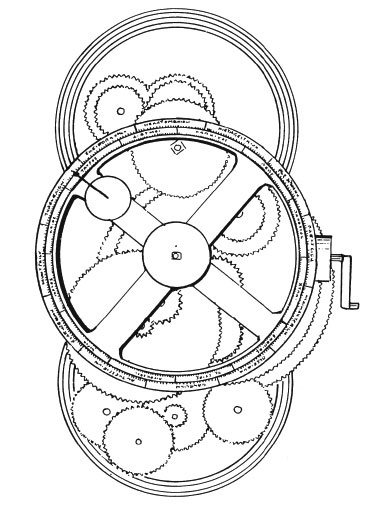
Антикитерский механизм и его реконструкция

Зубчатые колеса использовали еще древние греки для создания замечательного устройства – антикитерского механизма. В 1900 г. в окрестностях острова Антикитера ловец губок Элиас Стадиатис поднял с глубины 40 м бесформенную окаменелость, датированную примерно 65 г. до н. э. В 1902 г. археолог Валериос Стаис обнаружил, что в камне скрыты остатки зубчатого колеса и что на самом деле это часть сложного бронзового механизма. На нем были выгравированы слова, написанные буквами греческого алфавита. По имевшимся у ученых описаниям и форме объекта удалось определить, что это древний астрономический калькулятор. Он состоял минимум из 30 зубчатых колес (по последней реконструкции 2006 г. их было 37). Количество зубцов соответствовало основным астрономическим соотношениям. В частности, два колеса имели по 53 зубца – не самое простое число для изготовления детали. Оно соответствует частоте появления Луны на самом большом удалении от Земли по ходу ее орбиты. Все простые множители из числа зубцов были взяты из двух главных астрономических циклов: метонического и сароса. Рентгенологическое исследование выявило новые надписи и позволило их прочесть; теперь нет сомнений, что прибор использовался для определения положения Солнца, Луны и, возможно, всех известных тогда десяти планет. Эти надписи датируют 150–100 гг. до н. э.

Антикитерский механизм – сложнейший прибор, и, судя по всему, его создавали на основе теории Гиппарха о движении Луны. Вероятно, здесь не обошлось без участия его учеников. Также возможно, что прибор был игрушкой одного из членов царской семьи – судя по изощренности и дороговизне исполнения.

Третья важная тема «Исследований» – то самое открытие, которое подтолкнуло 19-летнего Гаусса посвятить всю свою жизнь математике: геометрическое построение правильного семнадцатиугольника (многоугольника с 17 сторонами). Евклид, использовавший линейку и циркуль, описал построение правильных многоугольников с тремя, четырьмя, пятью и пятнадцатью сторонами; он также знал, что эти числа сторон можно последовательно удваивать делением углов пополам, получая правильные многоугольники с шестью, восемью, десятью сторонами и т. д. Но Евклид не сумел построить многоугольники с семью или девятью сторонами – по сути, ни для одного числа, отличного от перечисленных выше. И на протяжении почти 2000 лет математики считали, что последнее слово осталось за Евклидом и невозможно построить иные правильные многоугольники. Гаусс опроверг это убеждение.

Укрощение бесконечности. История математики от первых чисел до теории хаоса - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 32

Онлайн книга - Укрощение бесконечности. История математики от первых чисел до теории хаоса | Автор книги - Йен Стюарт