
|
||
|
|
||
|
|
Онлайн книга - Боги Атлантиды. В поисках утраченных знаний | Автор книги - Колин Генри Уилсон
Cтраница 69

Но зачем Плантару понадобилось пускать пыль в глаза? Было очевидно, что изначально Плантар и Приорат Сиона намеревались привлечь к тайне внимание общественности, чтобы Франция вспомнила о потомках Меровингов в случае, если она устанет быть республикой. Де Сед сразу сказал Линкольну: «Мы надеялись на то, что все это заинтересует человека вроде вас» [158]. Когда Линкольн вгрызся в тему и обнаружил множество пятиугольников, Плантар решил, что тот продвигается слишком быстро, и решил пойти на попятную. В 1991 году Линкольн совершил еще одно важное открытие. Он познакомился с продюсером Эрлином Хаагенсеном, который работал на датском телевидении. Хаагенсен родился на острове Борнхольм и всегда восхищался 15 борнхольмскими церквями, которые были построены в XIII веке (во времена рыцарей-храмовников). Эти церкви часто сравнивали с древними мегалитами, которые действительно были встроены в их стены. В то время Линкольн размышлял, не связан ли рисунок Ренн-ле-Шато с мегалитической эпохой. Когда Хаагенсен рассказал ему о том, что борнхольмские церкви стоят в вершинах пятиугольников, Линкольн убедился в том, что каждый из них, как говорится, «разгадал свою часть общей загадки». Более того, Хаагенсен обнаружил, что в геометрии Борнхольма важную роль играет английская миля. Например, если геометрические построения Хаагенсена были верны, церкви Ибскер и Повлскер должны быть разделены ровно семью английскими милями. Так оно и было. Почему именно мили? В главе «Измерение» Линколь приводит несколько обескураживающих, но весьма убедительных фактов. Введенный в 1791 году французский метр составлял одну десятимиллионную от расстояния между Северным полюсом и экватором. Линкольн доказывает, что древнеанглийская мера длины, называвшаяся «rod», «pole» или «perch» (она составляет одну триста двадцатую мили), тоже связана с измерениями земной поверхности: один поул (198 дюймов), помноженный сам на себя (то есть в квадрате), дает километр (39 204 дюйма). Если этот древний поул (198 дюймов) помножить на 1,618, то есть на золотое сечение, мы получим 320, число поулов в миле. Таким образом, существует математическая связь между британским поулом и километром, а также между поулом, помноженным на золотое сечение, и милей. Кроме того, Линкольн цитирует «Историческую метрологию» Берримана, где утверждается, что греческий стадий доказывает: грекам был известен размер Земли. Берриман спрашивает: «Была ли Земля измерена в античный период?» — и показывает, что была, опираясь на примеры из Древнего Египта, Вавилона, Шумера, Китая, Персии и многих других культур. Он доказывает, что древние меры длины и веса восходят к размерам Земли, что, в свою очередь, означает, что древние люди уже измерили Землю. Современникам Берримана его сочинение должно было казаться безнадежно эксцентричным. Он утверждает, что многие меры длины были определенными частями земной окружности, что мера площади (акр) основывалась на десятой доле от радиуса Земли и что ряд весов базировался на плотности воды и золота. Создается впечатление, что Берриман постулирует существование каких-то древних цивилизаций, которые исчезли без следа, если не считать древних мер и весов. Все это, конечно же, как нельзя лучше сообразуется с замечанием Хэпгуда: история необязательно развивается по прямой. Развитие может стопориться, даже идти вспять. Отсюда Хэпгуд выводил и существование цивилизаций, которые достигли высот в науке 100 тысяч лет назад. Линкольну довелось познакомиться с норвежцем Харальдом Бёлке, который сделал замечательные открытия, изучая расстояния между населенными пунктами Норвегии. Тысячу лет назад Норвегия перестала быть языческой страной; с приходом христианства разбросанные тут и там деревни исчезали, уступая место крупным поселениям, которые превращались в города. Исследования Бёлке показывают, что эти новые города (Осло, Трондхейм, Берген, Ставангер, Хамар, Тонсберг) возводились словно бы на произвольно выбранных местах. Например, Осло был построен на болоте. Нет ни единой гипотезы касательно того, почему именно в Ставангере был возведен кафедральный собор. Однако расстояния между городами очень точны: от Осло до Ставангера — 190 миль, от Осло до Бергена — 190 миль, от Тонсберга до Ставангера — 170 миль, от Тонсберга до Хальсноя — 170 миль и так далее. Более того, древние монастыри расположены опять же в вершинах пятиугольников. Кажется, что когда Церковь христианизировала Норвегию, она действовала, исходя из принципов геометрии. Линкольн также вывел «церковную меру» (188 метров) и обратился через французский журнал с просьбой сообщить ему о том, где она встречается, равно как и о пента-гональной геодезии. Живущая во Франции учительница математики Патрисия Хокинс смогла обнаружить целых 162 «церковные меры», соединяющие церкви, холмы и придорожные распятия в области Кимпер в Бретани. 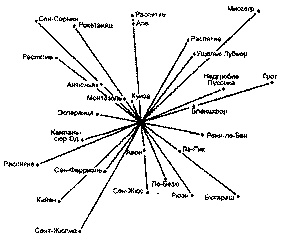
Все дороги ведут в Ренн-ле-Шато Последнюю главу книги «Ключ к священному узору» Линкольн начинает так; «Мы столкнулись с загадкой. Структуру ландшафта Ренн-ле-Шато и его связь с английской милей (как и очевидную связь этой мили с размерами Земли) легко продемонстрировать на множестве примеров. Меры длины и геометрия очевидны. Узоры повторяются. Образы полны смысла. Все это было создано в далеком прошлом, которое в свете подобного феномена предстает совершенно иным» [159]. Далее он умоляет историков и археологов обратить внимание на очевидное. Под «узорами» Линкольн понимает не просто пентакли холмов или круги церквей. Исследуя Ренн-ле-Шато, он выявил множество узоров, которые могли быть созданы лишь по чьей-то воле. «Священное место» тут — это «естественный пятиугольник холмов и рукотворный, структурированный Храм, который строили с расчетом включить в него этот пятиугольник» [160]. Я должен признаться, что убедить меня в чем-то нелегко. Мне достаточно бросить взгляд на расчерченную вдоль и поперек линиями карту, чтобы тяжело вздохнуть и закрыть книгу. Однако Линкольн сумел убедить меня в своей правоте. Например, он приводит схему, в центре которой расположена церковь Ренн-ле-Шато, соединенная линиями с близлежащими деревнями, церквями и замками. Прямой отрезок начинается с отдаленной церкви или замка, проходит через Ренн-ле-Шато и продолжается до другой церкви или замка. Одно из наиболее убедительных открытий Линкольна связано с прямоугольной сеткой. Если провести линии, соединяющие различные селения, окажется, что эти линии идут параллельно, и не только слева направо, но и сверху вниз. Более того, прямые разделяет одно и то же расстояние. 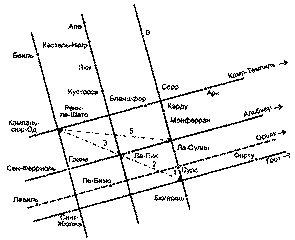
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно