Боги Атлантиды. В поисках утраченных знаний - читать онлайн книгу. Автор: Колин Генри Уилсон cтр.№ 68

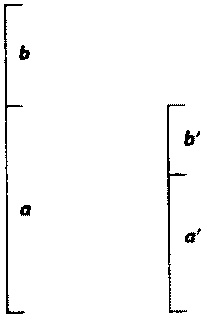
Золотое сечение

Художники используют золотое сечение, когда делают наброски, поскольку композиция картины, подчиняющаяся этому соотношению, радует глаз так же, как музыкальная гармония услаждает слух.

Почему природе нравится золотое сечение? Потому что это наилучший способ упаковать нечто, минимизировав занимаемое этим «нечто» пространство.

Может показаться, что золотое сечение описывается незамысловатой дробью, но это не так: в десятичном виде эта дробь 0,618034… продолжается до бесконечности.

В другой форме «фи» приближенно равно 1,618. Если вам нужно удлинить отрезок сообразно золотому сечению, просто умножьте его длину на 1,618.

Прежде чем вернуться к загадке Ренн-ле-Шато, еще немного математики. Существует названный по имени математика Фибоначчи ряд чисел, в котором каждое последующее число равно сумме двух предыдущих. Если начать с 0, следующим числом будет 1, затем 0+1 даст нам 1. Затем, если прибавить 1 к 1, мы получим 2. Прибавив 2 к 1, получим 3И так далее (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…).

Вот еще один интересный факт. Если взять два соседних числа Фибоначчи и разделить меньшее на большее, чем больше будут числа, тем ближе частное будет к золотому числу 0,618034… Например, если 2 разделить на 3, получится 0,6666… Но если 34 разделить на 55, получим 0,6182. Неважно, насколько велики числа Фибоначчи, пусть даже это будут миллионы и миллиарды, частное никогда не станет точно равно золотому числу.

Именно числа Фибоначчи можно обнаружить в годичных кольцах деревьев, раковинах моллюсков, спиральных туманностях. Почему Богу нравится золотое число — никто не знает. Стоит упомянуть о том, что спираль Фибоначчи можно вывести из пентакля. Если часть внутренней пентаграммы поместить под прямым углом к «ногам» пентакля, можно описать спираль Фибоначчи, начав с конца короткой линии.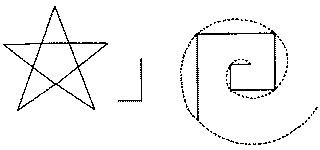

Спираль Фибоначчи

Кажется, Богу почему-то нравятся пентаграммы! Стоит добавить также, что, согласно Геродоту (в тексте, который мы немного подправим, устранив ошибку переписчика, делающую его абсурдным), золотое сечение можно найти в каждой грани пирамиды Хеопса.

Корнфорд объяснил Линкольну, что, изучая «Аркадских пастухов», искал одну из двух систем, которые постоянно использовали художники в ту эпоху. Первая — это система чисел, основанная на диалоге Платона «Тимей» (повествующем о создании вселенной) и очень популярная в эпоху Ренессанса. Вторая — куда более древняя геометрическая система, в основе которой лежит золотое сечение.

Корнфорд рассчитывал обнаружить на полотне Пуссена систему «Тимея», поскольку система золотого сечения считалась тогда ужасно старомодной. Он обнаружил следы системы чисел, но в общем и целом «Аркадские пастухи» базируются на золотом сечении. Кроме того, на картине скрыто множество пятиугольников.

Посмотрим вот на этот рисунок: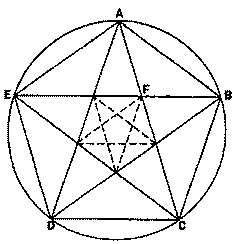

Пентаграмма в круге

Отношение каждой из пяти сторон пентаграммы (например, АВ) к ее хордам (скажем, АС) равно 1:1,618, или «фи».

Приглядевшись, Корнфорд обнаружил, что может нарисовать пентаграмму, которая выйдет за рамки картины: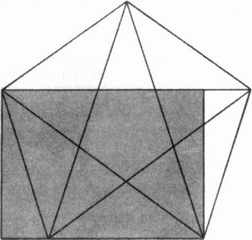

Пентаграмма, расширенная за рамки «Аркадских пастухов»

Если коротко, в картине Пуссена зашифрован пентакль. В итоге Корнфорд сделал любопытное замечание: возможно, фраза «у Пуссена есть ключ…» относится к местности вокруг Ренн-ле-Шато, где Соньер искал свои сокровища?

Это замечание привело Линкольна к одному из его важнейших открытий.

Бросив взгляд на топографическую карту окрестностей Ренн-ле-Шато, он сразу отметил, что три крупнейших населенных пункта (Ренн-ле-Шато, тамплиерский замок Безю и замок Бланшфор) являются тремя вершинами треугольника. Все они расположены на холмах.

Нарисовав на карте треугольник, Линкольн измерил его стороны и изумился. Треугольник получился идеально равнобедренным, проще говоря, две из трех его сторон оказались равны. Замок Безю располагается в вершине треугольника, от замка Бланшфор и от Ренн-ле-Шато его отделяет одно и то же расстояние.

Вряд ли это совпадение. Очень давно кто-то заметил, что вершины трех холмов образуют равнобедренный треугольник, и решил, что они подходят для некоего тайного замысла.

Линкольн задал себе вопрос: может быть, в округе найдутся по случайности еще два холма, образующие вместе с тремя упомянутыми холмами пентаграмму? Он понимал, что такого не бывает…

Однако, изучив как следует карту, Линкольн был ошеломлен: еще два холма были расположены точно там, где и следовало. Восточный холм именовался Ла-Сулан, западный — Сер-де-Лозе. Если эти пять холмов соединить линиями, получалась идеальная пентаграмма.

Удивительная игра природы! Но на этом сюрпризы не закончились. Посмотрев в центр карты, Линкольн обратил внимание на еще один холм, Ла-Пик

Надо сказать, что хотя на карте Ла-Пик помещается точно в центре пентаграммы, на деле он расположен в 250 ярдах к юго-востоку от ее центра. Но этого и следовало ожидать. В конце концов, мы имеем дело с нерукотворным ландшафтом. Достаточно чудесно уже то, что Ла-Пик расположен почти в центре пентаграммы.

Итак, вот и главная тайна Ренн-ле-Шато: эта деревня — часть священного ландшафта. Не исключено, что именно поэтому здесь поселился Дагоберт (а его сын Сигиберт бежал сюда после убийства отца). Королевская кровь Меровингов соединилась с волшебным ландшафтом.

Я был обуреваем сомнениями, пока не прочел книгу Линкольна «Key to the Sacred Pattern» («Ключ к священному узору») и не осознал, что речь идет о взаправдашнем «волшебном ландшафте», который увидел Генри Линкольн.

Как ни странно, Плантар отказался подтвердить правоту Линкольна. Было видно, как он и Шеризе пришли в ужас, когда Линкольн обнаружил пятиугольники на пергаментах Соньера, однако распространяться на эту тему Плантар не желал. С другой стороны, когда Линкольн стал расспрашивать его о скрытых шифрах на пергаментах, Плантар сказал удивительную вещь: пергаменты — это «приманка», состряпанная его товарищем Шеризе. Но с какой целью? Для десятиминутного фильма, снятого несколько лет назад.

Разумеется, Линкольн никак не мог в такое поверить. Необычайная сложность шифра не оставляла сомнений в том, что мастер своего дела придумывал этот шифр на протяжении долгого времени.