Математика в занимательных рассказах - читать онлайн книгу. Автор: Яков Перельман cтр.№ 9

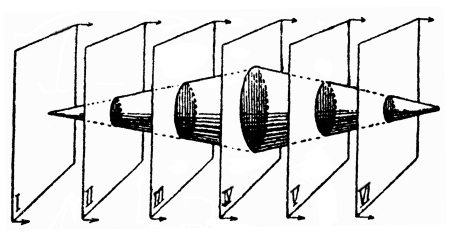
Рассмотрим еще пример. Двухмерный мир (плоскость), двигаясь в трехмерном пространстве, наткнулся на тело в форме двойного конуса (см. рис.). Двухмерный обитатель плоскости, конечно, не может воспринять этот конус как тело; не может даже и вообразить его себе. Что же будет он видеть и думать, когда мир его наткнется на подобное трехмерное тело, и оно пройдет сквозь плоский мир? Проследим за этим. Сначала в двухмерном мире появится точка — вершина конуса. Затем, по мере дальнейшего продвижения плоского мира в направлении третьего измерения (т. е. «с течением времени», как сказал бы двухмерный мыслитель), точка превратится в небольшой кружок или эллипс — сечение конуса плоскостью двухмерного мира. Кружок будет расти, расширяться и, достигнув наибольшего размера, станет сокращаться, постепенно превратится в точку и вновь исчезнет. Двухмерный исследователь наблюдал историю зарождения, развития, увядания и исчезновения «кружка», между тем как мы, существа трехмерные, воспринимаем ту же вещь сразу, одновременно в трех измерениях. Для них он существовал в ряде последовательно воспринимаемых плоских сечений, для нас — весь целиком, как трехмерное тело. Движение плоскости в третьем измерении знакомого нам пространства переживается двухмерным существом как течение времени. Для него «прошедшее» конуса — это те его части, которые лежат по одну сторону его плоского мира (по ту, откуда плоскость движется); «будущее» конуса — те его части, которые расположены по другую сторону, а «настоящее» — пересечение конуса с двухмерным миром.

Приложим теперь те же рассуждения к миру трехмерному. Когда мы описываем историю изменений какой-нибудь вещи в нашем трехмерном пространстве, не даем ли мы последовательные изображения этой вещи во времени? Если так, то можно рассматривать время как четвертое измерение мира, измерение, в котором движется наш трехмерный мир; каждое явление, наблюдаемое в трехмерном мире, есть одно из последовательных «пересечений» нашего трехмерного мира с четырехмерною вещью. Существо четырех измерений могло бы сразу охватить всю историю вещи, всю ее «жизнь» в виде некоторого четырехмерного объекта, недоступного нашему воображению.

Само собою разумеется, что фантастическая мысль Уэллса — придумать механизм для произвольного движения в четвертом измерении — не свободна от внутренних противоречий и должна быть принимаема не иначе как чисто художественный прием, удобный для успешного развития интриги фантастической повести.

Однажды, 27 июня, профессор Розетт бомбой влетел в общий зал, где собрались капитан Сервадак, лейтенант Прокофьев, Тимашев и ординарец Бен-Зуф.

— Лейтенант Прокофьев, — крикнул он, — отвечайте без обиняков и лишних разговоров на вопрос, который я вам задам.

— Я и не имею обыкновения… — начал было лейтенант.

— И отлично! — перебил профессор, обращавшийся с лейтенантом, как учитель с учеником. —

Отвечайте: вы объехали на вашей шхуне «Добрыне» кругом Галлии почти по экватору, иначе говоря — по ее большому кругу. Да или нет?

— Да, — ответил лейтенант, которому Тимашев подал знак не противоречить раздраженному ученому.

— Хорошо. А измерили вы при этом путь, пройденный шхуной?

— Приблизительно, т. е. с помощью лага и буссоли, но не измеряя высоты солнца и звезд, которую невозможно было определить.

— И что же вы узнали?

— Что окружность Галлии составляет около 2300 километров, а, следовательно, ее диаметр равен 720 километрам.

— Да, — сказал профессор, словно про себя: — диаметр в 16 раз меньше земного диаметра, равного 12 792 километрам. ^[11]

Сервадак и его спутники смотрели на ученого, не понимая, куда он ведет.

— Так вот, — оказал профессор, — для завершения моего изучения Галлии мне остается определить ее поверхность, объем, массу, плотность и напряжение тяжести на ней.

— Что касается поверхности и объема, — ответил Прокофьев, — то раз мы знаем диаметр Галлии, нет ничего легче, как определить их.

— А я говорю разве, что это трудно? — воскликнул профессор. — Ученик Сервадак, возьмите перо. Зная длину большого круга Галлии, определите величину ее поверхности.

— Вот, — ответил Сервадак, решивший держаться примерным учеником. — Множим окружность 2300 километров на диаметр, т. е. на 720. ^[12]

— Скорее же, — торопил профессор, — пора бы уже иметь результат. Ну!

— Так вот, — ответил Сервадак, — я получил в произведении 1 656 000 квадратных километров. Это и есть поверхность Галлии.

— Ну, — продолжал профессор, разгорячаясь, — а теперь, каков же объем Галлии?

— Объем… — замялся Сервадак.

— Ученик Сервадак, неужели вы не можете вычислить объем шара, раз вам известна его поверхность?

— Но, профессор, вы не даете мне времени вздохнуть…

— При вычислениях не дышат, сударь, не дышат!

Слушатели с большим трудом удерживались от смеха.

— Мы когда-нибудь кончим с этим? — спросил профессор. — Объем шара равен…

— Произведению поверхности на…

— На треть радиуса, сударь, на треть радиуса! — гремел профессор. — Кончили?

— Почти. Треть радиуса Галлии равна 120.

— Ну?

— Произведение 1 656 000 на 120 составляет 198 720 000 кубических километров.

— Итак, — сказал профессор, — мы знаем теперь диаметр, окружность, поверхность и объем

Галлии. Это уже нечто, но еще не все. Я намерен определить ее массу, плотность и напряжение тяжести на ее поверхности.

— Это будет трудно, — сказал Тимашев.

— Все равно. Я желаю знать, сколько весит моя комета, и узнаю это!

— Задача нелегкая, — заметил лейтенант Прокофьев. — Ведь нам неизвестен состав вещества Галлии.

— Вам неизвестен ее состав? — спросил профессор.

— Неизвестен, — сказал Тимашев, — и если вы нам поможете…