Математика в занимательных рассказах - читать онлайн книгу. Автор: Яков Перельман cтр.№ 19

Надо ли продолжать? Если 12-я шестеренка начнет вращаться только через двести миллионов лет, то когда дойдет очередь до 1000-й? Нетрудно вычислить. Число минут выразится числом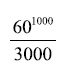

— числом, в котором 1775 цифр. Во всей Вселенной не хватит материи, чтобы дать материал для всех оттисков, число которых выражается 1779 цифрами. Ведь во Вселенной, по подсчетам специалистов (де-Ситера), «всего» 10⁷⁷ электронов, и даже если бы каждый оттиск состоял из одного электрона, можно было бы отпечатать лишь ничтожную долю всей продукции «литературной» машины. Перерабатывать старые оттиски вновь на бумагу? Но допуская даже при этом ничтожнейшую потерю материи в 1-биллионную долю, мы должны были бы иметь — считая снова по электрону на оттиск — число оттисков из 1767 цифр, а электронов у нас имеется число всего из 78 цифр…

Можно возразить, пожалуй, что незачем ждать окончания работы «литературной» машины: ведь шедевры литературы и замечательные открытия могут случайно оказаться среди первого миллиона оттисков. При невообразимо огромном числе всех возможных сочетаний эта вероятность еще более ничтожна, чем вероятность случайно наткнуться на один определенный электрон среди всех электронов Вселенной. Число электронов во Вселенной неизмеримо меньше, чем общее число возможных оттисков нашей машины.

Но пусть даже осуществилось несбыточное, пусть случилось чудо, и в наших руках имеется сообщение о научном открытии, появившееся из-под машины без участия творческой мысли. Сможем ли мы этим открытием воспользоваться?

Нет, мы даже не сможем признать этого открытия. Ведь у нас не будет критерия, который позволил бы нам отличить истинное открытие от многих мнимых, столь же авторитетно возвещаемых в процессе работы нашей машины. Пусть, в самом деле, машина дала нам отчет о превращении ртути в золото. Наряду с правильным описанием этого открытия будет столько же шансов иметь множество неправильных его описаний, а кроме того, описаний и таких невозможных процессов, как превращение меди в золото, марганца в золото, кальция в золото и т. д. и т. д. Оттиск, утверждающий, что превращение ртути в золото достигается при высокой температуре, ничем не отличается от оттиска, предписывающего прибегнуть к низкой температуре, причем могут существовать варианты оттисков с указанием всех температур от минус 273° до бесконечности. С равным успехом могут появиться из-под машины указания на необходимость пользоваться высоким давлением (тысячи вариантов), электризацией (опять тысячи вариантов), разными кислотами (снова тысячи и тысячи вариантов) и т. п.

Как при таких условиях отличить подлинное открытие от мнимого? Пришлось бы тщательно проверять на опыте каждое указание (кроме, конечно, явно нелепых), т. е. проделать такую огромную лабораторную работу, которая совершенно обесценила бы идеи «литературной» машины.

Точно так же пришлось бы проделать обширные исторические изыскания, чтобы проверить правильность каждого исторического факта, утверждаемого каким-нибудь продуктом механического производства открытий. Словом, ввиду полной невозможности отличать истину ото лжи, подобный «механический» способ двигать науку вперед был бы совершенно бесполезен, даже если бы каким-нибудь чудом удалось дождаться осмысленного оттиска.

Интересно отметить здесь следующий расчет Бореля (из книги «Случай»): вероятность выпадения орла 1000 раз подряд при игре в орлянку равна 2¹⁰⁰⁰, т. е. числу, содержащему около 300 цифр. Этот шанс приблизительно таков же, как и шанс получить две первых строки определенного стихотворения, вынимая наудачу из шапки буквы по следующему способу: в шапке 25 букв, одна из них вынимается, записывается и кладется обратно в шапку, после встряхивания вынимается вторая и т. д. Строго говоря, получить таким образом две первых строки определенного стихотворения вполне возможно. «Однако, — замечает Борель, — это представляется нам до такой степени маловероятным, что если бы подобный опыт удался на наших глазах, мы считали бы это плутовством». ^[32]

Высочайшая пирамида Древнего Египта — Хеопсова, уже пять тысячелетий обвеваемая знойным воздухом пустыни, представляет, без сомнения, самую удивительную постройку, сохранившуюся от Древнего мира. Высотою почти в полтораста метров, она покрывает своим основанием площадь в 40 тысяч квадратных метров и сложена из двухсот рядов исполинских камней. Сто тысяч рабочих в течение 30 лет трудились над возведением этого сооружения, — сначала подготовляя 10 лет дорогу для перевозки камней от каменоломни до места постройки, а затем громоздя их 20 лет друг на друга помощью несовершенных машин того времени.

Кажется странным, чтобы такое огромное сооружение воздвигнуто было с единственною целью — служить гробницею для правителя страны. Поэтому некоторые исследователи стали доискиваться: не раскроется ли тайна пирамиды из соотношения ее размеров?

Им посчастливилось, по их мнению, найти ряд удивительных соотношений, свидетельствующих о том, что жрецы, руководители работ по постройке, обладали глубокими познаниями по математике и астрономии и эти познания воплотили в каменных формах пирамиды.

«Геродот ^[33] рассказывает, — читаем мы в книге французского астронома Море (Загадки науки, 1926 г., т. I), — что египетские жрецы открыли ему следующее соотношение между стороною основания пирамиды и ее высотою: квадрат, построенный на высоте пирамиды, в точности равен площади каждого из боковых треугольников. Это вполне подтверждается новейшими измерениями. Вот доказательство, что во все времена пирамида Хеопса рассматривалась как памятник, пропорции которого рассчитаны математически.

Приведу более позднее доказательство: мы знаем, что отношение между длиною окружности и ее диаметром есть постоянная величина, хорошо известная современным школьникам. Чтобы вычислить длину окружности, достаточно умножить ее диаметр на 3,1416.