Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 53

Аппроксимация в виде x/log x хуже: в данном случае ее значение 48 254 942,4.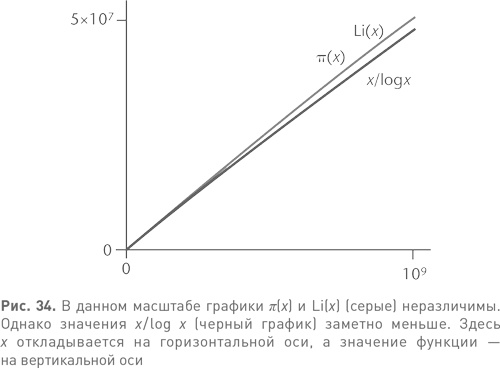

Приближенная формула с использованием Li(x) или x/log x стала известна как теорема о распределении простых чисел, где слово «теорема» использовалось в смысле «предположение». Поиск доказательства того, что эти формулы асимптотичны к π(x), стал одной из ключевых открытых задач теории чисел. Многие математики пытались одолеть ее при помощи традиционных методов этой области науки, и некоторые подошли к ответу достаточно близко, однако всегда оставалась какая-то хитрая посылка, которую никак не удавалось доказать. Нужны были новые методы. Они появились в результате любопытного переформулирования двух древних, еще евклидовых, теорем о простых числах.

Теорема о распределении простых чисел была ответом на евклидову теорему о том, что простые числа уходят в бесконечность и могут быть сколь угодно большими. Другая фундаментальная евклидова теорема говорит о единственности разложения на простые множители: каждое положительное целое число есть произведение простых чисел, причем только одного их набора. В 1737 г. Эйлер понял, что первую теорему можно переформулировать в виде поразительной формулы из действительного анализа, и тогда второе утверждение становится простым следствием этой формулы. Для начала я представлю формулу, а затем попытаюсь разобраться в ней. Вот она: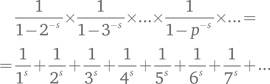

Здесь p принимает все простые значения, а s — константа. Эйлера интересовал в основном случай, при котором s — целое число, но его формула работает и для действительных чисел, в случае если s больше единицы. Это условие необходимо для того, чтобы ряд в правой части сошелся, т. е., будучи продолжен до бесконечности, принял бы осмысленное значение.

Это необыкновенная формула. В левой части мы перемножаем бесконечно много выражений, которые зависят только от простых чисел. В правой — складываем бесконечное число выражений, которые зависят от всех положительных целых чисел. Эта формула выражает, на языке анализа, некоторое отношение между целыми и простыми числами. Главное отношение такого рода — это единственность разложения на простые множители, именно она оправдывает существование формулы.

Я кратко опишу основной этап, чтобы показать, что за всем этим стоит разумная идея. Воспользовавшись школьной алгеброй, мы можем разложить выражение в ряд по p. Этот ряд напоминает правую часть формулы, но включает только степени p. А именно: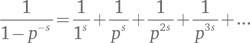

Когда мы перемножим все эти ряды, для всех простых p, и раскроем все скобки, мы получим комбинации с любыми степенями простых чисел, т. е. с любыми целыми положительными степенями. Все они выглядят как величины, обратные (т. е. единица, деленная на) s-й степени данного числа, и все возникают лишь единожды в связи с единственностью разложения на простые множители. Таким образом, получаем ряд в правой части.

Никому до сих пор не удалось найти простой алгебраической формулы для суммы этого ряда, хотя формул с интегралами немало. Поэтому мы присвоили ей особый символ — греческую букву дзета (ζ) — и определили новую функцию: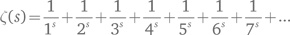

Вообще говоря, Эйлер не использовал символ ζ и рассматривал только положительные целые значения s, но я буду и дальше называть приведенный выше ряд эйлеровой дзета-функцией. Воспользовавшись своей формулой, Эйлер заключил, что существует бесконечно много простых чисел (для этого он рассматривал значения s, близкие к единице). Главной его целью было получить формулы вроде ζ (2) = π²/6 и найти сумму ряда для четных целых s. Развивать свою революционную идею дальше он не стал.

Другие математики заметили упущение Эйлера и рассмотрели нецелые значения s. В двух работах 1848 и 1850 гг. русский математик Пафнутий Чебышев предложил великолепную идею: попытаться доказать теорему о распределении простых чисел при помощи анализа. Начал он со связи между простыми числами и математическим анализом, обеспечиваемой эйлеровой дзета-функцией. Он не добился полного успеха, поскольку считал s действительным числом, а аналитические возможности действительного анализа весьма ограничены. Зато он сумел доказать, что для больших x отношение π(x) к x/log x лежит между двумя константами, одна из которых чуть больше единицы, а вторая — чуть меньше. Это был уже реальный результат, хотя пока еще не такой, как хотелось. Он позволил Чебышеву доказать постулат Бертрана, предложенный в 1845 г.: если взять любое натуральное число (≥2) и удвоить его, то между двумя этими числами обязательно найдется простое число.

Вот теперь сцена была готова к появлению Римана. Он тоже понял, что дзета-функция — это ключ к теореме о распределении простых чисел, но для реализации этого подхода ему пришлось предложить смелое расширение: определить дзета-функцию не только действительной, но и комплексной переменной. А начать можно с ряда Эйлера. Он сходится для любых действительных s больше единицы, и если использовать для комплексного s в точности ту же формулу, то ряд будет сходиться при любых s, у которых действительная часть больше 1. Однако Риман обнаружил, что можно сделать и лучше. Применив процедуру так называемого аналитического продолжения, он расширил определение ζ (s) на все комплексные числа, за исключением 1. Это значение s исключено потому, что при s = 1 значение дзета-функции становится бесконечным ^{30}.

В 1859 г. Риман собрал все свои мысли о дзета-функции в одну статью, заголовок которой можно перевести как «О количестве простых чисел, не превышающих заданной величины». В ней он привел полную и точную формулу π(x) ^{31}. Я опишу более простую формулу, эквивалентную римановой, чтобы показать, как появляются нули дзета-функции. Идея заключается в том, чтобы подсчитать, сколько простых чисел, или степеней простых чисел, укладывается до любого заданного предела. Однако вместо того чтобы сосчитать каждое число по одному разу, как функция π(x) делает с простыми числами, мы придаем большим простым числам дополнительный вес. Более того, любая степень простого числа учитывается в соответствии с логарифмом этого простого числа. Так, для предела 12 мы имеем следующие степени простых чисел: