Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 52

Если вы пытаетесь понять, как такое может быть, представим последовательность чисел — для некоего трудного для понимания свойства простых чисел — состоящую из степеней 100:

Но реальные числа при этом таковы:

т. е. лишняя единица сдвигается на каждом шаге влево на одну позицию. В этом случае отношение соответствующих чисел, чем дальше, тем ближе подходит к 1, а вот разность между ними приобретает вид:

и может достигать сколь угодно больших значений. Подобное поведение наблюдается в тех случаях, когда ошибка — разность между точным и приближенным ответом — беспредельно растет, но медленнее, чем растут сами числа.

Поиск асимптотических формул, имеющих отношение к простым числам, вдохновил математиков на создание новых методов теории чисел, основанных не на целых числах, а на комплексном анализе. Анализ — это строгое описание дифференциального и интегрального исчисления, включающего, как явствует из названия, два ключевых аспекта. В первом из них — дифференциальном исчислении — речь идет о скорости, с которой некая величина, называемая функцией, растет по отношению к другой величине. К примеру, положение тела зависит от времени, и скорость, с которой это положение изменяется со временем, представляет собой мгновенную скорость тела. Второй аспект — интегральное исчисление — имеет дело с расчетом площадей, объемов и тому подобных величин путем складывания большого числа очень маленьких кусочков. Процесс этот называется интегрированием. Примечательно, что интегрирование — это операция, обратная дифференцированию. Первоначальные формулировки Ньютона и Готфрида Лейбница требовали некоторых маневров с бесконечно малыми величинами, в связи с чем возникали вопросы о логической обоснованности этой теории. Со временем ученые разобрались с этими концептуальными вопросами, определив понятие предела — величины, к которой можно приблизиться на сколь угодно малое расстояние, но которой зачастую невозможно достичь. Именно в таком виде, в более строгих формулировках, метод получил название анализа.

Во времена Ньютона и Лейбница величины, о которых шла речь, представляли собой действительные числа, и результатом их работы, соответственно, стал действительный анализ. Когда же комплексные числа завоевали признание математиков, методы анализа естественным образом распространили и на них. Получился комплексный анализ, оказавшийся необычайно красивым и мощным инструментом. Вообще, когда дело доходит до анализа, комплексные функции ведут себя намного лучше, чем действительные. У них, конечно, есть свои особенности, но преимущества работы с комплексными функциями многократно перевешивают все их недостатки.

В какой-то момент математики с удивлением обнаружили, что арифметические свойства целых чисел можно с большой пользой переформулировать в терминах комплексных функций. До этого две системы ставили перед учеными очень разные вопросы и требовали использования очень разных методов. Но сегодня при помощи комплексного анализа — мощнейшего набора методик — можно открывать особые свойства функций теории чисел, а из них, в свою очередь, можно извлекать асимптотические формулы и многое другое.

В 1859 г. немецкий математик Бернхард Риман взял давнюю идею Эйлера и развил ее совершенно по-новому, определив так называемую дзета-функцию. Одним из результатов этой работы стала точная формула для количества простых чисел до заданного предела. Формула представляла собой бесконечную сумму, но специалистам по анализу к этому не привыкать. И это не было бесполезной игрой ума: благодаря этой формуле удалось получить новые подлинные знания о мире простых чисел. Мешала только одна маленькая неувязка. Хотя Риман мог доказать, что его формула точна, самые важные потенциальные следствия из нее полностью зависели от одного простого утверждения, касающегося дзета-функции, и вот это-то простое утверждение Риман никак не мог доказать. И сегодня, полтора столетия спустя, мы все еще не сумели сделать это. Сегодня это утверждение называется гипотезой Римана и представляет собой, по сути, священный Грааль чистой математики.

В главе 2 мы видели, что простые числа обыкновенно встречаются тем реже, чем они больше. Поскольку казалось, что точных формул для их распределения наверняка не существует, возникало естественное желание поискать статистические закономерности. В 1797–1798 гг. Лежандр подсчитал, сколько простых чисел помещается в натуральном ряду вплоть до различных пределов. Для этого он воспользовался таблицами простых чисел, которые незадолго до того составили Георг Вега и Антон Фелькель. Веге, судя по всему, вообще нравились сложные расчеты: он составил таблицы логарифмов и в 1789 г. стал обладателем мирового рекорда по вычислению числа π, которое он посчитал до 140-го десятичного знака (из них 126 были посчитаны верно). А Фелькелю просто нравилось искать простые числа. Его главная работа вышла в 1776 г. и называлась «Таблица всех простых делителей чисел до 10 000 000, за исключением тех, что делятся на 2, 3 или 5». Для проверки делимости на 2, 3 и 5 есть простые способы, упомянутые в главе 2, и он сэкономил в книге много места, опустив эти числа. Лежандр открыл эмпирическую приближенную формулу для количества простых чисел, меньших заданного числа x, и обозначил это количество π(x). Если вы привыкли воспринимать π только как символ для обозначения числа 3,14159, это потребует привыкания, но в любом контексте несложно понять, что именно имелось в виду, даже если вы не заметили, что символы даны в несколько разном начертании. В 1808 г. в тексте Лежандра по теории чисел утверждалось, что значение π(x), судя по всему, очень близко к значению выражения x/(log x − 1,08366).

В 1849 г. в письме к астроному Иоганну Энке Гаусс сообщил, что в свое время, лет в 15, сделал на полях таблицы логарифмов запись, в которой утверждалось количество простых чисел, меньших или равных x, составляет x/log x для больших x. Гаусс не опубликовал это наблюдение (как и многие другие свои открытия), возможно, потому, что не имел доказательства. В 1838 г. Дирихле сообщил Гауссу об аналогичной приближенной формуле, найденной им самим. По существу, эта формула сводится к логарифмической интегральной функции ^{29}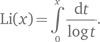

По мере того как x становится большим, отношение Li(x) к x/log x стремится к 1; это означает, что если одно из них асимптотически равно π(x), то асимптотически равно и второе, но рис. 34 позволяет предположить (совершенно верно), что Li(x) — лучшее приближение, чем x/log x. Точность Li(x) впечатляет. К примеру,