Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 33

Нерешетчатые укладки — совершенно иное дело. Их бесконечно много, и они не отличаются приятной регулярностью структуры. Почему бы нам не удариться в другую крайность и не попробовать случайную укладку? Стивен Гейлс в своем труде «Статика растений» (1727) рассказал об экспериментах, в ходе которых он «вжимал несколько пакетов свежего гороха в один горшок» и обнаруживал, что при сильном сдавливании они образуют то ли «красивые правильные додекаэдры», то ли «достаточно правильные додекаэдры» ^[4]. Судя по всему, автор говорил о том, что правильные додекаэдры красивы, а не о том, что додекаэдры получались довольно правильные, но вторая интерпретация лучше, потому что настоящими правильными додекаэдрами невозможно без пустот заполнить пространство. Вероятно, он видел перед собой ромбические додекаэдры, которые, как мы уже убедились, связаны с гранецентрированной кубической решеткой. Дэвид Скотт насыпа́л в контейнер множество шариков от подшипников, тщательно встряхивал и измерял плотность укладки. По его данным, максимально она равнялась 0,6366. В 2008 г. Сун Чаомин, Ван Бин и Эрнан Макс получили эту же величину аналитически. Однако их результат не подразумевает, что Кеплер был прав, хотя бы потому, что это означало бы, что гранецентрированная кубическая решетка с плотностью 0,74 не может существовать. Простейшее объяснение такого расхождения заключается в том, что их результат не учитывает чрезвычайно редкие исключения, при том что и гранецентрированная кубическая, и гексагональная решетки, и все бесчисленные варианты конструкций из треугольных слоев представляют собой именно такие исключения. По тому же принципу может существовать и еще какая-нибудь конструкция с еще большей плотностью. Это не может быть регулярная конструкция, но найти ее при помощи бессистемного поиска невозможно, ибо ее вероятность равна нулю. Так что исследование случайных вариантов упаковки, хотя и важно для многих областей физики, не слишком много говорит нам о гипотезе Кеплера.

Первый по-настоящему важный прорыв в решении этой задачи произошел в 1892 г., когда Аксель Туэ в ходе лекции на Скандинавском конгрессе естественных наук коротко изложил доказательство того, что никакая упаковка кругов на плоскости не может быть плотнее треугольной решетки. Лекция была опубликована, но формулировки там слишком неопределенны, чтобы можно было реконструировать само доказательство. Новую версию того же доказательства Туэ опубликовал в 1910 г. Оно казалось убедительным, за исключением нескольких технических моментов, которые, как считал автор, можно было без особого труда довести до ума. Но Ласло Фейеш Тот, вместо того чтобы заполнять пробелы в чужом доказательстве, получил в 1940 г. собственное, полное, основанное на других методах. Вскоре после этого Беньямино Сегре и Курт Малер представили альтернативные доказательства. А в 2010 г. Чан Хайчау и Ван Личун выложили в Интернет более простое доказательство.

Задача поиска наибольшей плотности укладки кругов или шариков при определенных условиях относится к классу математических задач, известных как задачи оптимизации. В такой задаче предлагается найти максимальное или минимальное значение некоторой функции (т. е. математического правила вычисления некой величины, которая определенным образом зависит от некоего набора переменных). Правило вычисления функции часто задается формулой, но это не обязательно. К примеру, таким образом можно сформулировать задачу с 49 кругами на плоскости. Переменными здесь будут координаты центров всех 49 кругов, а поскольку на каждый круг потребуется по две координаты, всего переменных получится 98. Сама функция — это размер наименьшего квадрата со сторонами, параллельными координатным осям, в который можно поместить данный набор неперекрывающихся кругов. Задача эквивалентна поиску минимального значения, которое принимает эта функция при значениях переменных, соответствующих всем вариантам решетки.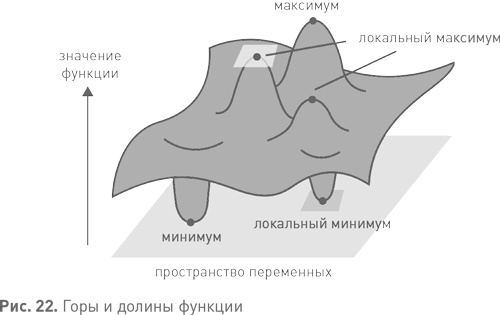

Функцию можно представить в виде многомерного ландшафта, каждая точка на котором соответствует определенному набору переменных, а высота в этой точке — значению функции. Максимум функции — это высота самого высокого ее пика, а минимум — глубина самой глубокой долины. В принципе задачи оптимизации можно решать методами дифференциального исчисления: в максимуме или минимуме функция должна быть горизонтальна (см. рис. 22), и дифференциальное исчисление позволяет отразить это условие в уравнении. Чтобы решить задачу укладки кругов в квадрат этим методом, нам пришлось бы решить систему из 98 уравнений с 98 переменными.

Решение задач оптимизации встречает на пути одно неожиданное препятствие: подобные уравнения часто имеют большое количество решений. Ландшафт может иметь множество локальных максимумов, из которых самый высокий лишь один. Представьте себе, к примеру, Гималаи: кроме пиков, там почти ничего и нет, но лишь Эвересту принадлежит рекорд высоты. Методы поиска пиков, самый очевидный из которых звучит как «иди вверх, пока это возможно», часто выводят на локальные максимумы и застревают на них. Еще одна трудность состоит в том, что с ростом числа переменных растет и вероятное число локальных пиков. Тем не менее иногда такой метод срабатывает. Даже частичные результаты могут оказаться полезными: если вам удалось найти локальный пик, ясно, что настоящий максимум не может быть ниже. Именно так была найдена улучшенная раскладка кругов в квадрате.

Для регулярных укладок функция, максимум которой нужно найти, зависит от конечного числа переменных — направлений и длин, вдоль которых решетка повторяется. Для нерегулярных укладок функция зависит от бесконечно большого числа переменных — центров всех кругов или шариков. В подобных случаях прямое использование дифференциального исчисления и других методик оптимизации ничего не даст. Доказательство Тота основано на хитрой идее переформулировать задачу о нерегулярной упаковке кругов и превратить ее в задачу оптимизации с конечным набором переменных. Позже, в 1953 г., он понял, что тот же трюк в принципе можно проделать и с гипотезой Кеплера. К несчастью, получившаяся функция зависит примерно от полутора сотен переменных — слишком много для ручного расчета. Но Тот прозорливо разглядел возможный выход: «Имея в виду стремительное развитие наших компьютеров, можно предположить, что минимум можно будет определить с высокой точностью».

В то время вычислительная техника только начинала развиваться, и достаточно мощной машины попросту не существовало, так что в последующие годы работа над гипотезой Кеплера шла в других направлениях. Ряд математиков занимался уточнением верхней границы для возможного значения плотности сферической упаковки. К примеру, в 1958 г. Роджерс доказал, что плотность не превосходит 0,7797. И никаких исключений: эта оценка относилась к любым способам укладки шариков. В 1986 г. Дж. Линдси понизил этот предел до 0,77844, а Дуглас Мадер в 1988 г. чуть-чуть улучшил оценку и получил 0,77836. Эти результаты показали, что невозможно получить плотность намного выше, чем 0,7405, характерные для гранецентрированной кубической решетки. Но тем не менее пробел в доказательстве сохранялся.