Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 31

Если мы работаем всего лишь с двумя слоями, разница между двумя вариантами не играет никакой роли. Мы можем без труда получить первый вариант укладки, просто повернув второй вариант на 60°. Эти варианты одинаковы «с точностью до симметрии». Но после укладки первых двух слоев у нас появляются два по-настоящему разных варианта для третьего слоя. Каждый новый слой имеет две системы выемок, показанных на рис. 19 слева светлыми и темными точками. В одной из них выемки соответствуют центрам шариков предыдущего слоя, которые на рис. 19 справа видны как светло— серые треугольнички. Во второй выемки соответствуют выемкам предпредыдущего слоя и видны на рис. 19 справа как треугольнички с вписанными в них крохотными белыми шестиугольничками. Чтобы получить гранецентрированную кубическую решетку, мы должны использовать для третьего слоя темно-серые позиции, а затем повторять такой порядок укладки до бесконечности.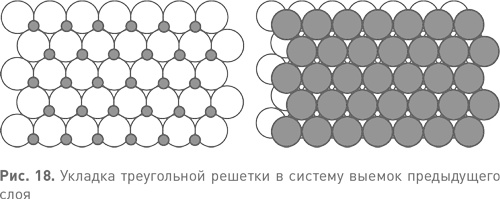

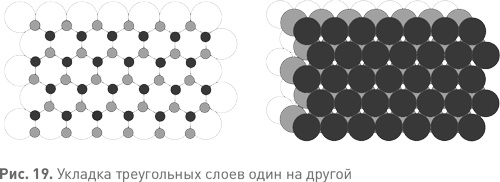
Не до конца очевидно, однако, что результатом такой укладки станет гранецентрированная кубическая решетка. Где же здесь квадраты? Дело в том, что квадраты в такой укладке присутствуют, но располагаются наклонно, под углом. На рис. 20 показаны шесть последовательных треугольных слоев, из которых удалена часть шариков. Стрелками указаны ряды и столбцы скрытой внутри квадратной решетки. Все слои, параллельные данному, тоже выстроены по квадратной решетке, а между собой соотносятся в точности так же, как я выстраивал гранецентрированную кубическую решетку.

Насколько компактна такая упаковка? Мы измеряем компактность (эффективность) упаковки ее плотностью: долей общего объема, занимаемой шариками ^{20}. Чем больше плотность, тем компактнее упаковка. Кубики укладываются в параллелепипед с плотностью 1, заполняя весь объем. Между шариками, очевидно, в любом случае останутся промежутки, так что плотность их упаковки меньше единицы. Плотность гранецентрированной кубической решетки составляет в точности π/√18, это примерно 0,7405. При такой упаковке шарики заполняют чуть меньше трех четвертей пространства, и гипотеза Кеплера утверждает, что никакая упаковка шариков не может иметь плотность больше этой.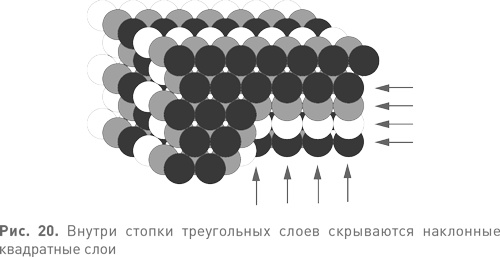

Я сформулировал все это достаточно осторожно. Я не сказал, что «плотность гранецентрированной кубической решетки выше, чем любой другой». Такое утверждение было бы неверным, и в этом несложно убедиться. Для этого вернемся к построению гранецентрированной кубической решетки из треугольных слоев. Я сказал, что после укладки первых двух слоев возникает два варианта укладки третьего. Гранецентрированная кубическая решетка возникает во втором варианте — том, что с темно-серыми точками. Что произойдет, если мы пойдем по первому пути и используем светло-серые точки? Тогда шарики третьего слоя окажутся точно над шариками первого. Продолжив точно так же и помещая каждый новый слой точно над позапрошлым слоем, мы получим второй вариант объемной решетки: гексагональную. Она отличается от гранецентрированной кубической решетки, но имеет ту же плотность. Интуитивно это понятно, поскольку два разных способа укладки третьего слоя симметричны относительно поворота, а сам слой в обоих случаях ложится на предыдущий одинаково плотно.

Это единственные два способа решетчатой упаковки, которые можно получить при укладке стопки треугольных слоев, но в 1883 г. географ и кристаллограф Уильям Барлоу заметил, что для каждого следующего слоя мы можем произвольно выбрать любой из двух вариантов укладки. Поскольку оба варианта вносят в плотность всей стопки одинаковый вклад, плотность всех этих вариантов упаковки будет одинакова и равна π/√18. При этом существуют бесконечно много случайных последовательностей такого рода и, соответственно, бесконечно много различных вариантов упаковки с одинаковой плотностью.

Короче говоря, нет единственной самой плотной объемной упаковки шариков. Их бесконечно много, и все они одинаково плотные. Отсутствие единственно верного решения — предупреждение: проблема не так проста и прямолинейна. Если Кеплер был прав, то существует оптимальная плотность упаковки, но есть и бесконечное множество различных структур, ею обладающих. И чтобы доказать оптимальность этой плотности, недостаточно успешно пристраивать каждый новый шарик к предыдущим как можно плотнее. Есть варианты.

Конечно, торговцы фруктами обладают невероятно богатым опытом — ведь гранецентрированную кубическую решетку наверняка можно было увидеть на рынках Древнего Египта еще в додинастическую эпоху, — но одним лишь опытом в таком деле никак не обойдешься. Вообще, тот факт, что метод торговцев фруктами дает хороший результат, в определенной мере случайность. Задача торговца фруктами состоит не в том, чтобы упаковать апельсины как можно плотнее в пространстве, где возможна, в принципе, любая конструкция. Его задача — уложить плоды как можно надежнее в мире, где земля плоская, а сила тяжести действует сверху вниз. Поэтому торговец начинает с того, что выкладывает апельсины в один слой — это очень естественно; затем он добавляет сверху еще один слой и т. д. Если ящик, в который укладываются плоды, прямоугольный, то первый слой, скорее всего, будет выложен по квадратной решетке. Если площадь ничем не ограничена, то естественной будет либо квадратная, либо треугольная решетка. В конечном итоге обе дают гранецентрированную кубическую решетку — по крайней мере, если треугольные слои укладываются как следует. Вообще говоря, квадратная решетка представляется не лучшим вариантом — ведь это не самый плотный способ укладки одного слоя. Однако — скорее по счастливой случайности, чем в результате осознанного выбора — это, как оказалось, не имеет значения.

Физики не интересуются апельсинами, их больше занимает то, как соседствуют друг с другом атомы. Кристалл — это регулярная, пространственно периодическая конструкция из атомов. Гипотеза Кеплера утверждает, что периодичность кристалла — это естественное следствие максимально плотной «упаковки» атомов. Для большинства физиков само существование кристаллов является достаточным доказательством, — по их мнению, гипотеза Кеплера очевидно верна. Однако мы только что убедились, что существует бесконечно много способов упаковки шариков с точно такой же плотностью, как у гранецентрированной кубической и гексагональной решеток, и что способы эти не являются пространственно периодическими. Так почему в кристаллах природа использует именно периодические структуры? Возможно, ответ в том, что атомы не следует рассматривать как сферические объекты.