Путеводитель для влюблённых в математику - читать онлайн книгу. Автор: Эдвард Шейнерман cтр.№ 35

Таким образом, нам придется проделать максимум 99 × 99 = 9801 операцию. Это гораздо лучше первого метода, но все еще неэффективно. Если сравнение и смена позиции требует двух секунд, я закончу спустя пять часов. Это никуда не годится.

И вот я в расстроенных чувствах выхожу из кабинета, чтобы развеяться. В коридоре я встречаю двух постдоков, которые работают под моим научным руководством. Зловещая улыбка змеится на моих губах. Я спешу обратно в кабинет, делю стопку неотсортированных тетрадей пополам и даю по 50 тетрадей каждому постдоку. «Вот вам стопка тетрадей, – говорю я. – Пожалуйста, рассортируйте их по алфавиту и принесите ко мне в кабинет, когда закончите». После чего с воодушевлением возвращаюсь к основной работе ^[129].

Мне предстоит доделать сортировку, когда постдоки выполнят задание. Нужно превратить две упорядоченные стопки в одну. Насколько это будет трудно? Допустим, у меня есть две стопки тетрадей в алфавитном порядке. Я смотрю на верхние тетради в той и другой стопке, выбираю первую по алфавиту и кладу в итоговую стопку. Диаграмма иллюстрирует процесс.

Когда одна из стопок иссякает, я просто-напросто кладу оставшуюся в конец итоговой стопки. В худшем случае придется проделать 99 операций. Это потребует всего несколько минут!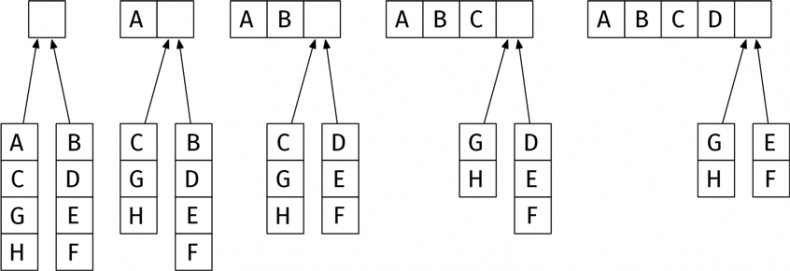

Но как насчет моих постдоков? У каждого стопка с 50 тетрадями. Постдоки – люди смышленые, поэтому не станут сортировать тетради самостоятельно. Они, в свою очередь, поделят свои стопки пополам (таким образом, в каждой окажется по 25 тетрадей) и передоверят сортировку аспирантам! Когда те закончат, постдокам останется соединить две отсортированные стопки по 25 тетрадей в одну общую по 50. Это потребует максимум 49 операций.

Но четыре аспиранта тоже не дураки. Они делят свои стопки на две части (в одной 12, в другой 13 тетрадей) и находят восемь старшекурсников, чтобы передоверить работу. В результате каждому аспиранту остается соединить две маленькие стопки и отдать их постдокам.

Как старшекурсники сортируют тетради? Несложно догадаться: они делят свои стопки на две части (в одной 6 тетрадей, в другой 7), ловят 16 третьекурсников и отдают им эти стопки. Те находят 32 второкурсника и отдают им раздербаненные стопки (в одних по 3, в других по 4 тетради). Наконец, второкурсники отлавливают 64 первокурсника и отдают им стопки по 1 и по 2 тетради. Первокурсникам делать нечего: они быстро сортируют свою часть и отдают обратно.

Очевидно, эта «схема Понци ^[130]» экономит мое время, но насколько она эффективна в целом? Посмотрим, как много операций она потребует в худшем случае. Занесем все данные в таблицу: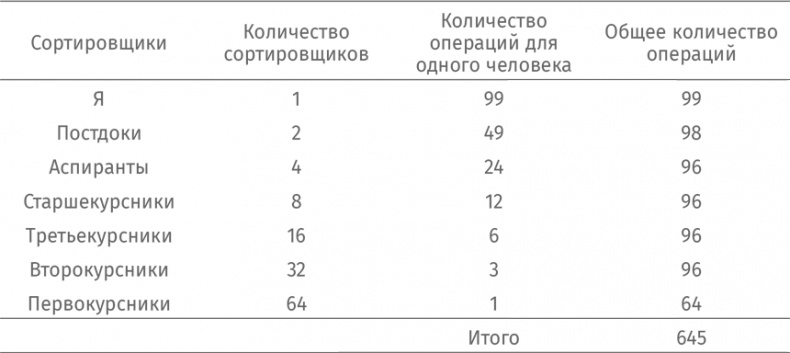

Максимальное количество операций оказывается существенно меньше, чем при сортировке пузырьковым методом.

К несчастью, в этой схеме есть изъян: у меня сейчас нет постдоков! Так что вместо вербовки целой армии помощников придется работать самому.

Для начала я найду большой незагроможденный стол. Я поделю стопку из 100 тетрадей пополам и положу две стопки по краям стола. Как я их отсортирую? По тому же алгоритму! Поделю две стопки по 50 тетрадей на четыре по 25, а их буду сортировать тем же методом. В худшем случае понадобится 645 операций. Правда, на сей раз мне придется действовать в одиночку. Однако это лучше, чем почти что 10 000 операций при сортировке пузырьковым методом.

Словарное определение не должно включать определяемого слова. Вообразите, что вы ищете в словаре слово оскудение и находите такое определение:

Что за чушь! Однако наш алгоритм сортировки и слияния грешит именно этой ссылкой на самого себя. Вот более точное определение.

Алгоритм, ссылающийся сам на себя, называют рекурсивным. В отличие от неудачного определения слова оскудение, наш алгоритм работает, потому что рано или поздно дойдет до конечной точки. Когда-нибудь множество объектов сведется к одному, и больше не придется проделывать процедуру заново. Поэтому нет опасности уйти в «бесконечный цикл».

Наибольший общий делитель

Каково наибольшее среди чисел, на которые нацело делятся одновременно 986 и 748? Простейший способ ответить на вопрос – перепробовать все варианты. Разумеется, 986 и 748 делятся на 1. Несложно видеть, что на 2 они тоже делятся. Но ни то ни другое число не делится на 3. Одно из них, 748, делится на 4, а другое нет. Нам «всего-навсего» нужно перебрать все делители и сравнить их. Мы остановимся после 748, потому что дальше числа не могут быть делителями 748. Наконец мы выясним, что у 748 и 986 четыре общих делителя: 1, 2, 17 и 34. Наибольший общий делитель 748 и 986 равен 34. Для любых положительных целых чисел a и b запись НОД (a, b) означает их наибольший общий делитель ^[133].

Описанный выше метод дает незамысловатый и неоспоримый алгоритм поиска наибольшего общего делителя. Его слабая сторона – неэффективность. Для поиска НОД двух трехзначных чисел придется перебрать сотни вариантов. Может быть, есть что-нибудь попроще?