
|
||
|
|
||
|
|
Онлайн книга - Путеводитель для влюблённых в математику | Автор книги - Эдвард Шейнерман
Cтраница 33

Или: f(ab) = f(a) + f(b). (*) Новый вопрос: какого рода функция удовлетворяет этому правилу и условиям f(1) = 0 и f(10) = 1? Что дают логарифмы [122]? Некоторые математические операции можно проделать наоборот. Например, мы возводим в квадрат какое-нибудь число: 6² = 36. А теперь проделываем обратную операцию – извлекаем квадратный корень:
Например, 10⁴ = 10 000. Мы проделываем наоборот операцию возведения в степень и применяем логарифмическую функцию [123]: lg(10 000) = 4. Можно воспринимать логарифмическую функцию как ответ на вопрос: «В какую степень возводить?» В какую степень нужно возвести 10, чтобы получить некое число? Скажем, какая степень 10 дает 1000? Поскольку 1000 = 10 × 10 × 10 = 10³, ответ равен 3. Иными словами, lg(1000) = 3. Несложно уяснить, что происходит, когда мы возводим 10 в степень, равную целому положительному числу, – мы просто перемножаем 10 заданное число раз: 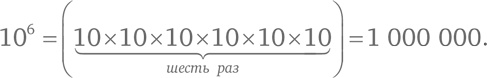
Если мы посчитаем нули в одной из степеней 10, то поймем значение логарифма: lg(1 000 000 000) = 9. Возведение 10 в дробную степень несколько сложнее. Ключевая идея здесь – понять, чему равно произведение 10m и 10ⁿ. Чему равно произведение 10⁶ × 10⁵? Не бойтесь, перемножать десятки просто. Давайте распишем нашу формулу: 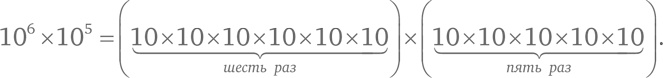
Каков результат? Нет нужды перемножать! Просто посчитайте, сколько раз встречается 10 в правой части формулы: одиннадцать. Иными словами, 10⁶ × 10⁵ = 1011. Таким образом, для целых положительных степеней 10m × 10ⁿ = 10m + ⁿ. Это тождество называется законом умножения степеней. Ключевая идея вычисления дробной степени – применение данного закона для любых показателей степени. Давайте посмотрим, к чему это приведет. Возьмем 100,5. Мы можем не знать, чему оно равно, но нам известно, чему равно произведение 100,5 × 100,5. А именно: 100,5 × 100,5 = 100,5 + 0,5 = 10. Если умножить 100,5 само на себя, получится 10. Таким образом, 100,5 равно квадратному корню из десяти [124]: 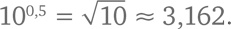
Так мы можем посчитать все степени 10. На рисунке вы видите график функции 10х при x от 0 до 1. При каком значении x выполняется условие 10х = 2? При взгляде на график функции 10х кажется, что подойдет x = 0,3. Если мы возьмем калькулятор, то выясним: 100,3 ≈ 1,99526… Близко, но не равно точно 2. Чуть-чуть увеличим степень. Попробуем x = 0,301; результат 100,301 ≈ 1,99986… Ближе, но все еще мимо цели. Нам нужно число немного больше. Величина x должна быть равна 0,30102999566398114… Это и будет log(2). (Вы уже встречали такое число раньше. Отыщите его!) Закон умножения степеней 10m × 10ⁿ = 10m + ⁿ можно переформулировать для логарифмов. Посмотрим, как такое сделать. Допустим, a = 10m и b = 10ⁿ. Чему равен десятичный логарифм a? Это степень, в которую нужно возвести 10, чтобы получить a. Иными словами, lg(a) = m. Аналогично lg(b) = n. 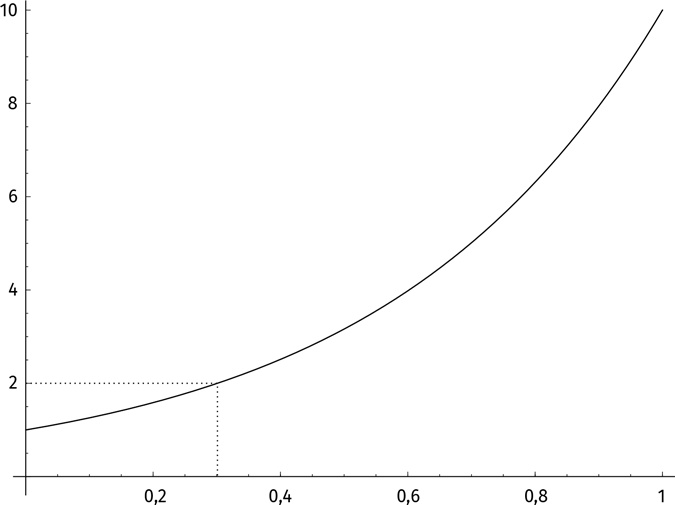
Чему равен логарифм произведения ab? Мы знаем, что a = 10m и b = 10ⁿ. Таким образом, ab = 10m + ⁿ. В какую степень нужно возвести 10, чтобы получить ab? Ответ: m + n. На языке математических символов это выглядит так: lg(ab) = m + n. Подытожим: lg(a) = m, lg(b) = n, lg(ab) = m + n. Отсюда мы выводим закон сложения для логарифмов: lg(ab) = lg(a) + lg(b). (**) Похоже, мы уже встречали эту формулу… Завязываем узелки Давайте подытожим то, что мы узнали из предыдущих разделов. Мы определили функцию f(m) как долю тех величин среди большого количества измерений, мантисса которых меньше m. Эта функция удовлетворяет трем условиям: f(1) = 0, f(10) = 1, f(ab) = f(a) + f(b). Потом мы обсудили логарифмы и выяснили следующее: lg(1) = 0, lg(10) = 1, lg(ab) = lg(a) + lg(b). Другими словами, значения f при 0 и 10 совпадает со значением десятичного логарифма от тех же величин. Кроме того, f и логарифм подчиняются одному и тому же правилу в соответствии с формулами (*) и (**). На основе этих фактов (и чисто технической оговорки, что функция f непрерывна) математики могут доказать, что f представляет собой логарифмическую функцию.
|
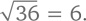 Для положительных чисел операции возведения в квадрат и извлечения квадратного корня обратны друг другу. Операция, обратная возведению в степень, называется извлечением логарифма.
Для положительных чисел операции возведения в квадрат и извлечения квадратного корня обратны друг другу. Операция, обратная возведению в степень, называется извлечением логарифма. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно