
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 7

Задача 1.9
Наименьшее число, которое делится на первые девять целых чисел, равно 2520. Какое наименьшее число будет делиться на первые 13 целых чисел? Обычный подход
Проще всего найти все множители для первых 13 целых чисел и перемножить их. Это, правда, потребует много времени и утомительных вычислений. Не забывайте, что множители нельзя повторять (например, множитель 8 недопустим, поскольку 4 и 2 уже использовались). Так или иначе, данный метод позволяет в конечном итоге получить правильный ответ, если, конечно, все сделать тщательно и без ошибок. Образцовое решение
Теперь попробуем порассуждать. Очевидно, что множители от 1 до 9 (первые девять целых чисел) уже использовались для получения произведения, равного 2520. Следовательно, нам нужно рассмотреть только целые числа 10, 11, 12 и 13, поскольку число 2520, задействующее предыдущие целые числа, уже известно. Множители 10 (5 × 2) и 12 (4 × 3) уже использовались. Однако 11 и 13 — это простые числа, которые делятся только сами на себя и на 1. Таким образом, умножив 2520 × 11 × 13, мы определяем, что наименьшее число, которое делится на первые 13 целых чисел, равно 360 360. Задача 1.10
Ал, Барбара, Кэрол и Дэн сдают экзамен по математике. В целом они правильно ответили на 67 вопросов, и у каждого из них есть как минимум один правильный ответ. Ал дал больше всего правильных ответов. Барбара и Кэрол дали в сумме 43 правильных ответа. Сколько правильных ответов дал Дэн? Обычный подход
Обычно делают предположение для каждого участника экзамена, проверяют, не нарушаются ли условия задачи, и смотрят, дают ли предположения в сумме 67. Такой подход может дать правильный ответ, однако все очень зависит от удачности предположений. Образцовое решение
Применим нашу стратегию логического рассуждения. Поскольку Барбара и Кэрол вместе дали 43 правильных ответа, у одной из них таких ответов должно быть, как минимум, 22, а у другой — 21. Так как Ал оказался впереди всех, то с учетом предыдущих предположений в отношении Барбары и Кэрол у него должно быть, как минимум, 23 правильных ответа. Если допустить, что у Ала 23 правильных ответа, у Барбары — 22, а у Кэрол — 21, то в сумме у них будет 23 + 22 + 21 = 66 правильных ответов. Это означает, что Дэн правильно ответил только на один вопрос. Поскольку у всех есть как минимум один правильный ответ, результат 1 для Дэна правилен. Задача 1.11
Лайза, которая едет на велосипеде по мосту, соединяющему точки A и B, и уже преодолела
Обычный подход
Поскольку длина моста неизвестна, зададим ее произвольно, выбрав какое-нибудь удобное (хотя, может быть, и нереалистичное) число, скажем, 8 км. Если Лайза поедет назад, к началу моста (точка A), со скоростью y км/ч, то она преодолеет 3 км за
Если Лайза поедет к точке B, то аналогичным образом мы получим уравнение
Объединив эти два уравнения, мы получим 8y = 300–180 = 120, а следовательно, y = 15. Таким образом, максимальная скорость Лайзы равна 15 км/ч. Образцовое решение
Стратегия логического рассуждения дает более изящное решение. Раз Лайза впритык успевает доехать до любого конца моста, будем считать, что она едет вперед к точке B. К тому моменту, когда поезд подойдет к точке A, она преодолеет еще
Задача 1.12
Если S = 1! + 2! + 3! + 4! + 5! + … + 98! + 99! то какая цифра в числе S будет находиться в разряде единиц? |
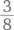 его длины, слышит, что сзади приближается поезд, движущийся со скоростью 60 км/ч. Она прикидывает расстояния и решает, что впритык сможет избежать столкновения, если поедет в любую сторону (к точке A или точке B) максимально быстро. Какова ее максимальная скорость?
его длины, слышит, что сзади приближается поезд, движущийся со скоростью 60 км/ч. Она прикидывает расстояния и решает, что впритык сможет избежать столкновения, если поедет в любую сторону (к точке A или точке B) максимально быстро. Какова ее максимальная скорость?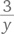 часа. За это время поезд пройдет x км от точки A. Данный отрезок времени можно представить, как
часа. За это время поезд пройдет x км от точки A. Данный отрезок времени можно представить, как
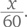 Это дает нам уравнение:
Это дает нам уравнение:
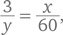 или xy = 180.
или xy = 180.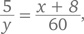 или xy + 8y = 300.
или xy + 8y = 300.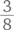 пути, т. е. всего
пути, т. е. всего
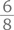 длины моста (или
длины моста (или
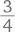 его длины). Теперь ей нужно проехать оставшуюся
его длины). Теперь ей нужно проехать оставшуюся
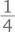 моста за то же самое время, которое требуется поезду, чтобы преодолеть полную длину моста. Таким образом, ее скорость равна
моста за то же самое время, которое требуется поезду, чтобы преодолеть полную длину моста. Таким образом, ее скорость равна
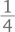 скорости поезда, т. е. 15 км/ч.
скорости поезда, т. е. 15 км/ч. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно