
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 6

Поскольку периметр треугольника численно равен его площади, мы получаем:
Задача 1.5
В США президентов выбирают каждые четыре года в годы, кратные 4. Некоторые из этих лет являются также квадратами целых чисел. Сколько президентских выборов между 1788 и 2016 годами пришлось на годы, которые являются квадратами простых чисел? В каких годах они проводились? Обычный подход
Один из путей решения этой задачи — перебор всех четырехлетних периодов между 1788 и 2016 г. Поскольку 1788 делится на 4, то это будет первый год президентских выборов в рассматриваемом диапазоне. Таким образом, можно составить перечень этих лет (1788, 1792, 1796, …, 2012, 2016), а затем извлечь квадратный корень из каждого для определения тех лет, которые являются квадратами целых чисел. Калькулятор, конечно, облегчит задачу, но процесс решения все равно будет долгим и нудным! Образцовое решение
Это отличный пример применения стратегии логического рассуждения. Прежде всего, кратным 4 может быть только четный год, поэтому можно отбросить все нечетные годы. Помимо этого, квадратные корни из этих лет должны лежать в интервале от 40 до 50, поскольку: 402 = 1600 (до заданного диапазона); 422 = 1764 (до заданного диапазона); 442 = 1936; 462 = 2116 (после заданного диапазона). В пределах заданного диапазона находится только 1936 г. Таким образом, 1936 — это единственный год президентских выборов, который является квадратом целого числа. Задача 1.6
Джимми подбрасывает одновременно две монетки. Он делает это до тех пор, пока хотя бы на одной монетке не выпадет орел (О). На этом игра заканчивается. Какова вероятность того, что в последнем подбрасывании орел выпадет на обеих монетках? Обычный подход
Первая реакция — это взять две монетки и посмотреть, какими будут результаты после большого числа подбрасываний. Вместе с тем, как и в большинстве вероятностных экспериментов, пространство выборок чаще всего оказывается слишком маленьким, чтобы предсказать результат с приемлемой точностью. Образцовое решение
Обратимся к стратегии логического рассуждения. При выполнении этого эксперимента все предыдущие подбрасывания монеток не имеют значения. Значение имеет только одно подбрасывание, в результате которого выпадает орел (О). Поэтому ограничимся анализом только этого последнего подбрасывания. Возможными являются четыре варианта: 
В трех из этих четырех вариантов выпадает как минимум один орел. Орел не выпадает только в одном варианте — его можно отбросить. Единственный вариант с двумя орлами — это ОО. Таким образом, вероятность составляет
Задача 1.7
У одних пород свиней рождаются поросята с двумя завитками на хвостах, у других пород — с тремя завитками. Фермер поручает своим детям подсчитать, сколько свиней находится в свинарнике. Дети, одержимые математикой, сообщают ему, что количества свиней с двумя завитками и с тремя завитками выражаются простыми числами, а общее количество завитков на хвостах равно 40. Сколько свиней в свинарнике фермера? Обычный подход
Если взять за x количество свиней с двумя завитками на хвостах, а за y — количество свиней с тремя завитками, то мы получаем уравнение 2x + 3y = 40. Это одно уравнение с двумя неизвестными. Числа здесь сравнительно невелики, поэтому можно попробовать найти ответ путем подстановки различных значений x и y. Вместе с тем, поскольку известно, что x и y простые числа, выбор ограничивается следующими величинами: 19, 17, 13, 11, 7, 5, 3 и 2. В любом случае процесс решения довольно длителен, скучен и громоздок. Образцовое решение
Если взять за x количество свиней с двумя завитками на хвостах, а за y — количество свиней с тремя завитками, то 2x + 3y = 40, как мы уже говорили. Однако на этот раз пойдем дальше и проанализируем полученное уравнение, опираясь на логику. Поскольку и 40, и 2x — четные числа, четным числом должен быть и y, иначе сумма (40) не будет четной. Поскольку y — простое число, он должен быть равен 2 (это единственное четное простое число), а 3y должно равняться 6. Теперь решим уравнение для x: 2x + 6 = 40, 2x = 34, x = 17. У фермера в свинарнике 17 + 2, или 19 свиней. Задача 1.8
Число называют «специальным», если оно делится на сумму составляющих его цифр. Какое из следующих чисел удовлетворяет этому условию? 11, 111, 1111, 11111, 111111, 1111111, 11111111, 111111111. Обычный подход
Обычно мы подсчитываем сумму цифр в каждом числе и делим число на эту сумму. Например, 11 должно делиться на 1 + 1, или на 2. Но оно не делится на 2, поэтому 11 не является специальным числом. Если действовать таким образом, то нам придется решить восемь небольших задачек. Образцовое решение
Хотя описанный выше подход в конечном итоге позволяет решить задачу, воспользуемся логическим рассуждением для поиска более изящного решения. Прежде всего, очевидно, что все приведенные числа являются нечетными, поскольку ни одно из них не оканчивается на 2, 4, 6, 8 и 0. Четное количество единиц даст нам четную сумму. Это позволяет отбросить числа с четной суммой единиц: 11, 1111, 111111 и 11111111. Помимо этого, число 11111 не делится на 5, поскольку оно не оканчивается на 0 или 5. Если проверить число 1111111, то окажется, что оно не делится на 7. В результате у нас остаются всего два числа. Число 111 делится на 3, т. е. на сумму входящих в него цифр (3 × 37). Аналогичным образом число 111111111 делится на 9 (т. е. 9 × 12 345 679). Таким образом, 111 и 111111111 являются двумя «специальными» числами в приведенном числовом ряду. |
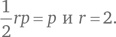
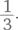
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно