Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 59

Если мы рассмотрим отношение частот смежных нот, то оказывается, что В:А относится как 9:8. Отношения между D и С, так же как и G:F, равны 9:8. Отношения E:D и A:G — не совсем такие же, но очень близки — 10:9. Другими словами, из семи интервалов между нотами в пределах одной октавы пять имеют примерно равный размер; мы можем назвать их «целыми интервалами».

Частотное отношение F:E, однако, является только половинкой, поскольку оно равно 352:330, или 16:15; это также истинно и для отношения С:В. (Более просто можно объяснить это другими словами. Отношение 9:8 представляет собой увеличение в частоте на 12,5 процента, а отношение 10:9 представляет собой увеличение на 11,1 процента. Однако отношение 16:15 представляет собой увеличение только на 6,7 процента.) То есть при переходе от В к С или от Е к F мы преодолеваем только «половину интервала» ^[56].

Если мы начнем с А и будем подниматься по октаве вверх через ноты В, С и так далее, то мы будем проходить интервалы в следующем порядке: тон, полутон, тон, тон, полутон, тон, тон, тон, полутон, тон, тон, полутон и так далее. Полутона последовательно отделены двумя целыми тонами, затем — тремя целыми тонами, двумя тонами, тремя тонами и так далее.

Когда мы поем гамму, используя традиционные имена для нот (до, ре, ми, фа, соль, ля, си, до), благодаря многовековой привычке мы настаиваем на размещении полутоновых интервалов между ми и фа и между си и до. Любая другая последовательность кажется нам звучащей неправильно. Таким образом, мы хотим, чтобы семь интервалов октавы располагались по следующему образцу: тон, тон, полутон, тон, тон, тон, полутон. Если вы посмотрите назад, то увидите, что такая специфическая последовательность может существовать, только если мы начинаем гамму с ноты до, то есть до на ноте С (на которой из С — не имеет никакого значения). Тогда ре становится D, ми — Е, фа — F, соль — G, ля — А, си — В и снова до становится С. Малый интервал «ми — фа», в котором расстояние между нотами равно полутону, переписывается в EF, а интервал «си — до», в котором расстояние равно тому же полутону, соответствует ВС. Расположение нот, которые вы поете, теперь соответствует последовательным нотам, из которых состоит октава, если начинать ее с С и играть на белых клавишах фортепьяно. Если вы начнете играть ноты на любой другой клавише, кроме С, и будете нажимать последовательно белые клавиши, то и фортепьяно, и вы будете извлекать полутона в непривычных местах, а потому — звучание (фортепьяно, конечно, а не ваше) будет казаться вам ужасным.

Желательно быть способным играть гамму от любой точки на клавиатуре фортепьяно, например, для того, чтобы приспособить диапазон фортепьяно к конкретному человеческому голосу. По этой причине в каждую октаву вставлены пять черных нот, расстояния между «белыми» клавишами и «черными» клавишами равны одному полутону, что позволяет разбить любую октаву на пять больших интервалов. Это позволяет нам сохранить привычную последовательность двух (CD, DE) и трех тонов (FG, GA, АВ) — тон, тон, полутон, тон, тон, тон, полутон — по всей клавиатуре. Теперь можно начинать играть гамму с любой клавиши фортепьяно, не важно — с черной или с белой; не забывайте только выбирать ноты тщательно и нажимать иногда черную, а иногда белую. И только если вы начинаете с С, вы можете сыграть всю гамму, всего лишь нажимая последовательно белые клавиши.

Именно по той причине, что С оказывается естественной до, игра в «ключе С» является самой простой для начинающих (главным образом — только белые клавиши). До первой октавы ^[57] является специфической нотой, которая находится примерно в середине клавиатуры фортепьяно, частота этой ноты равна 264/с ^[58].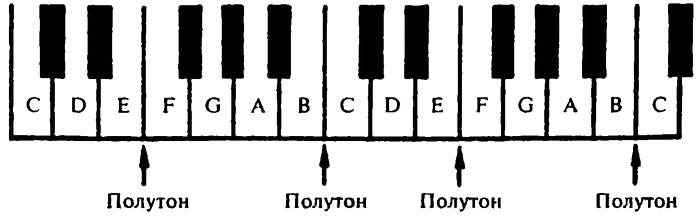

^{Клавиатура фортепьяно}

Высота тона изменяется, если источник звука перемещается относительно слушателя. Предположим, что стоящий вдалеке поезд издает гудок, который имеет частоту 344/с. В этом случае, когда звуковая волна достигает нас, в нашу барабанную перепонку каждую секунду будут ударять 344 комбинации сжатия/разрежения. Поскольку звук (при комнатной температуре) двигается со скоростью 344 метра в секунду, последовательные области сжатия будут располагаться на расстоянии одного метра.

Предположим теперь, что поезд начинает быстро двигаться по направлению к нам со скоростью 34,4 метра в секунду (75,8 мили в час), или, иначе, — со скоростью, равной одной десятой скорости звука. Он все еще продолжает издавать гудок. Одна область сжатия перемещается перед ним; ко времени, когда она переместилась на один метр, испускается другая область сжатия. Однако к этому времени поезд продвинулся вперед на десятую часть метра, и вторая область сжатия будет находиться на расстоянии только 0,9 метра позади первой. Если поезд движется с постоянной скоростью, то же самое происходит и со всеми остальными последовательными областями сжатия. По этой причине наших барабанных перепонок достигает сначала первая область, а затем — следующая, но звуковые волны исходят от движущегося поезда, а потому вторая волна достигнет наших барабанных перепонок на 0,1 секунды раньше, то есть до нас доходит 344/0,9, или 382 колебания. Человек, едущий на поезде и поэтому перемещающийся вместе с источником звука, получает за одну секунду все те же 344 области сжатия. Отношение 382:344 близко к 9:8, так что звук гудка поезда представляется более пронзительным для человека, наблюдающего подход поезда, чем для человека, который едет на поезде, и разница составляет почти целый тон.

С другой стороны, если поезд удаляется от слушателя, то за то время, когда первая область сжатия переместилась на метр к слушателю, возникает новая область, поезд отдалится на десятую часть метра и расстояние между двумя областями сжатия будет 1,1 метра. Частота звука составит тогда 344/1,1, или 312 раз в секунду. Теперь это ниже почти на целый тон, чем было бы слышно человеку на поезде.

Если бы мы стояли на перроне, то звук гудящего и проносящегося мимо нас поезда изменился бы внезапно: от частоты 382/с по мере приближения и прохождения к частоте 312/с по мере удаления. Это явление называется эффектом Доплера, названным так в честь австрийского физика Иоганна Кристиана Допплера (1803–1853), который первым изучил и дал правильное объяснение данному эффекту в 1842 году.